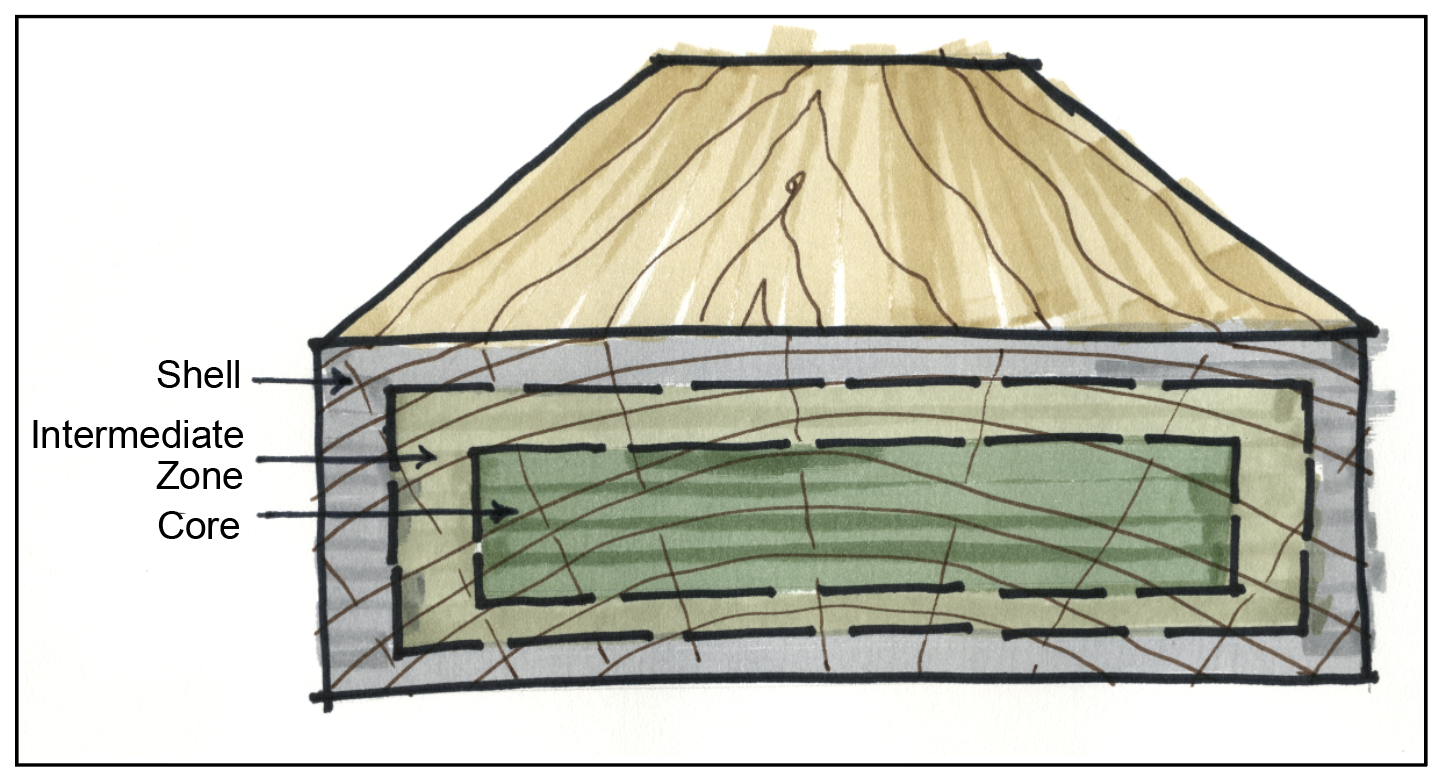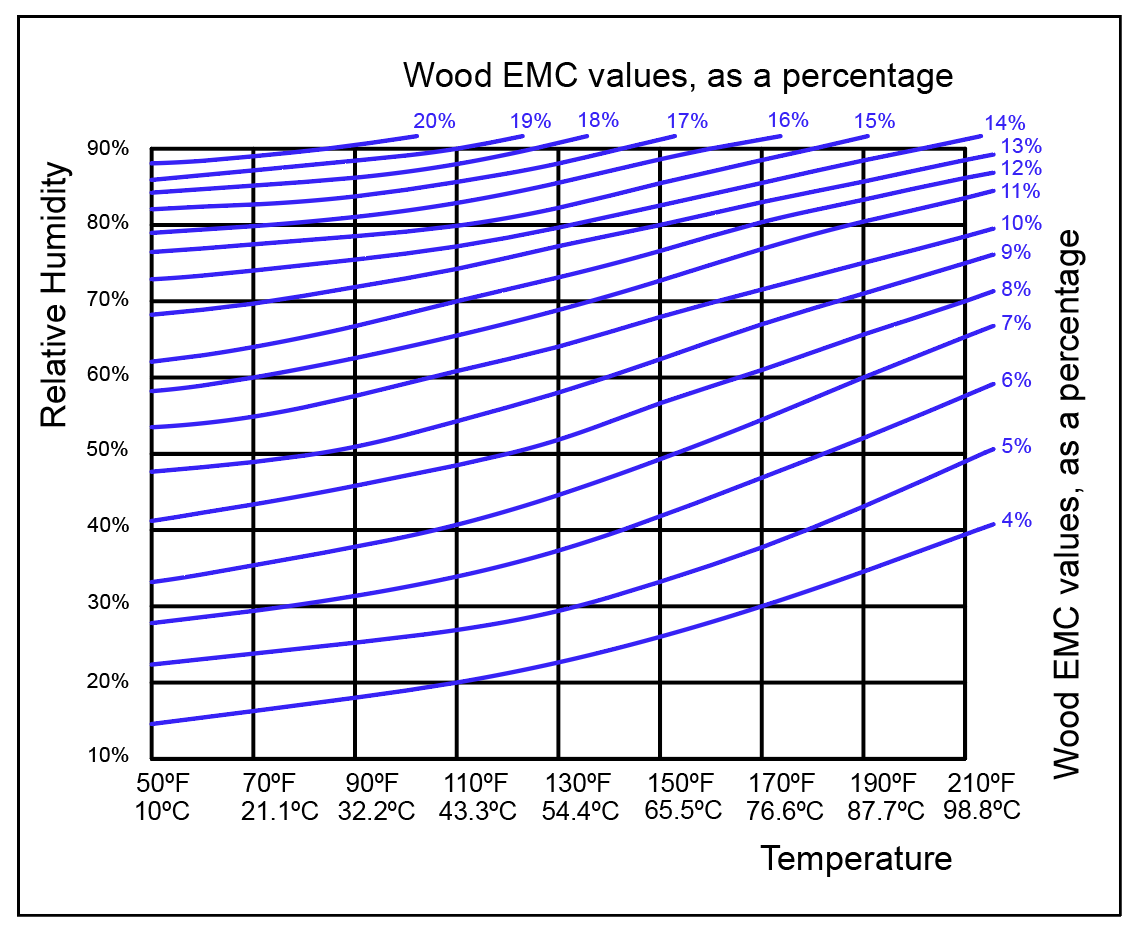
The following in excerpted from “Cut & Dried: A Woodworker’s Guide to Timber Technology,” by Richard Jones.
The author has spent his entire life as a professional woodworker and has dedicated himself to researching the technical details of wood in great depth, this material being the woodworker’s most important resource. The result is this book, in which Richard explores every aspect of the tree and its wood, from how it grows to how it is then cut, dried and delivered to your workshop.
Richard explores many of the things that can go right or wrong in the delicate process of felling trees, converting them into boards, and drying those boards ready to make fine furniture and other wooden structures. He helps you identify problems you might be having with your lumber and – when possible – the ways to fix the problem or avoid it in the future.
“Cut & Dried” is a massive text that covers the big picture (is forestry good?) and the tiniest details (what is that fungus attacking my stock?). And Richard offers precise descriptions throughout that demanding woodworkers need to know in order to do demanding work.
In order to design successful structures we furniture makers and other woodworkers need to develop some understanding of wood’s strength. It is common knowledge amongst experienced woodworkers that some woods are stronger than others; we quickly learn both European oak or American white oak are stronger than balsa wood, or ash is a better material for hammer shafts than European red pine, i.e., Scots pine. But the question to pose is, “What determines the strength of wood?” The answer lies in the material’s ability to resist stress, and the strain or deformation resulting from the stress along with the material’s ability, or inability, to recover its original form when, or if, the stress is removed. Both stress and strain are definable and measurable.
Stress, more precisely described as unit force, is the amount of force acting on a defined area; strength is the ability of a material to resist unit force. Stronger materials resist unit force better. It’s relatively easy to work out the unit force a bookshelf must resist. To do so, weigh the books carried by a shelf to establish the load (L) and calculate the shelf’s surface area (A). The numbers for the following sample calculations came from a convenient load of books on a shelf in my home.
• 42 books weighed on domestic scales = 32 kg (or 71 lbs). Shelf dimensions: 870 mm x 295 mm = 0.26 M² (or 34.25″ x 11.61″ = 2.76 ft²).
• To calculate the unit force (UF) applied to the shelf, divide the load (L) by the area (A) thus: L / A: therefore 32 kg / 0.26 sq m = 123.01 kg per sq m UF.
• Working in pounds and feet calculate: L / A: therefore 71 lb / 2.76 sq ft = 25.72 lb per sq ft UF. This can be converted to pounds per square inch (PSI) thus: 25.72 / 144 sq in = 0.18 PSI.
Engineers and scientists seek greater accuracy than the methodology used here of weighing with bathroom scales and rounding results to two decimal places, but the methodology and values used illustrate the principle. Additional calculations using the source data shows the shelf carries approximately 11.04 kg per 300 mm length, or approximately 24.69 lb per foot length. My experience is these numbers are typical; for many years I have used 25 lb per foot length or 11 kg per 300 mm length as standard bookshelf loading. There are exceptions furniture makers have to design for, but those exceptions are generally readily spotted, e.g., a request to create shelving for a collection of large-format art books immediately triggers a reaction that the shelving should be stronger. For example, you might use 18 mm thick solid oak instead of 18 mm thick oak veneered MDF, or extra reinforcement is necessary, or the shelf span should be shortened, or a combination of all three measures may the right solution.
It is possible, where necessary, to calculate the load beams are likely to experience in use, then to design for and build in enough strength for the intended load, plus an additional safety margin. Situations where woodworkers are most likely to recognise the necessity for such calculations are in the building or construction industry, e.g., safe loading of wooden floors and roof truss design. Indeed, there are calculations, formulae and standard load tables used by structural engineers to account for the load-bearing requirements of such structures.
Posts, such as music stands, easels, benches and table legs, chair legs, parasols and umbrellas, cabinet sides etc., all experience loads or stress. In many cases each individual leg in a chair is more than strong enough to carry the weight of a person; the design challenge for a one-legged pedestal chair is finding a way of supporting the pedestal so it doesn’t fall over when applying a downward load and, further, making it strong enough to cope with any torsional (twisting or rotational stress) and horizontal forces a pedestal chair leg must endure.
Stressed parts, i.e., loaded parts, experience strain and strained parts deform; strain is defined as unit deformation. If you lightly tap the surface of a piece of 50 mm- (2″-) thick wood with a hammer the wood directly under the hammer head compresses, i.e., the thickness reduces and this illustrates unit deformation. After a very gentle tap with a hammer, the wood will regain its original shape and form showing the wood is elastic and it can recover if not unduly stressed. Without controlled laboratory conditions it is hard to measure the amount of compression but under a light load as just described let us assume, for the purpose of an example, the unit deformation is 0.2 mm (0.00787 inches).
Calculating the unit deformation caused by the impact of the hammer head requires the sum: Dimensional Change / Original Dimension
Using the figures given in the hammer-tapping example, i.e., original plank thickness = 50 mm and the amount of compression = 0.2 mm the calculation is: 0.2 mm / 50 mm = 0.004 millimetre per millimetre (mm/mm). The end result is expressed here as millimetre per millimetre, meaning 0.004 millimetre (unit deformation) per millimetre (of thickness), the same proportion as 0.2 / 50. In reality the expression “millimetre per millimetre” is not necessary from an engineer’s perspective because the proportion of deformation, i.e., 0.004 to the original thickness of the piece of wood is the key information. The same rule applies when you work in any other unit of measure as long as the same units are used on both sides of the equation, e.g., inches divided by inches, metres divided by metres, miles divided by miles etc. The following sum uses inches but note the end result is still 0.004.
After converting the metric measurements used in the previous paragraph to three decimal places in inches, the sum and the result are: 0.008 in / 2 in = 0.004 inches per inch (in/in). Dimensional change is 0.004 inch per inch.
Returning now to hitting the wood with a hammer, tapping the surface of the wood harder and harder with the hammer will eventually lead to one of those blows leaving a noticeable and permanent dent in the wood. This rough and ready experiment demonstrates Hooke’s Law.
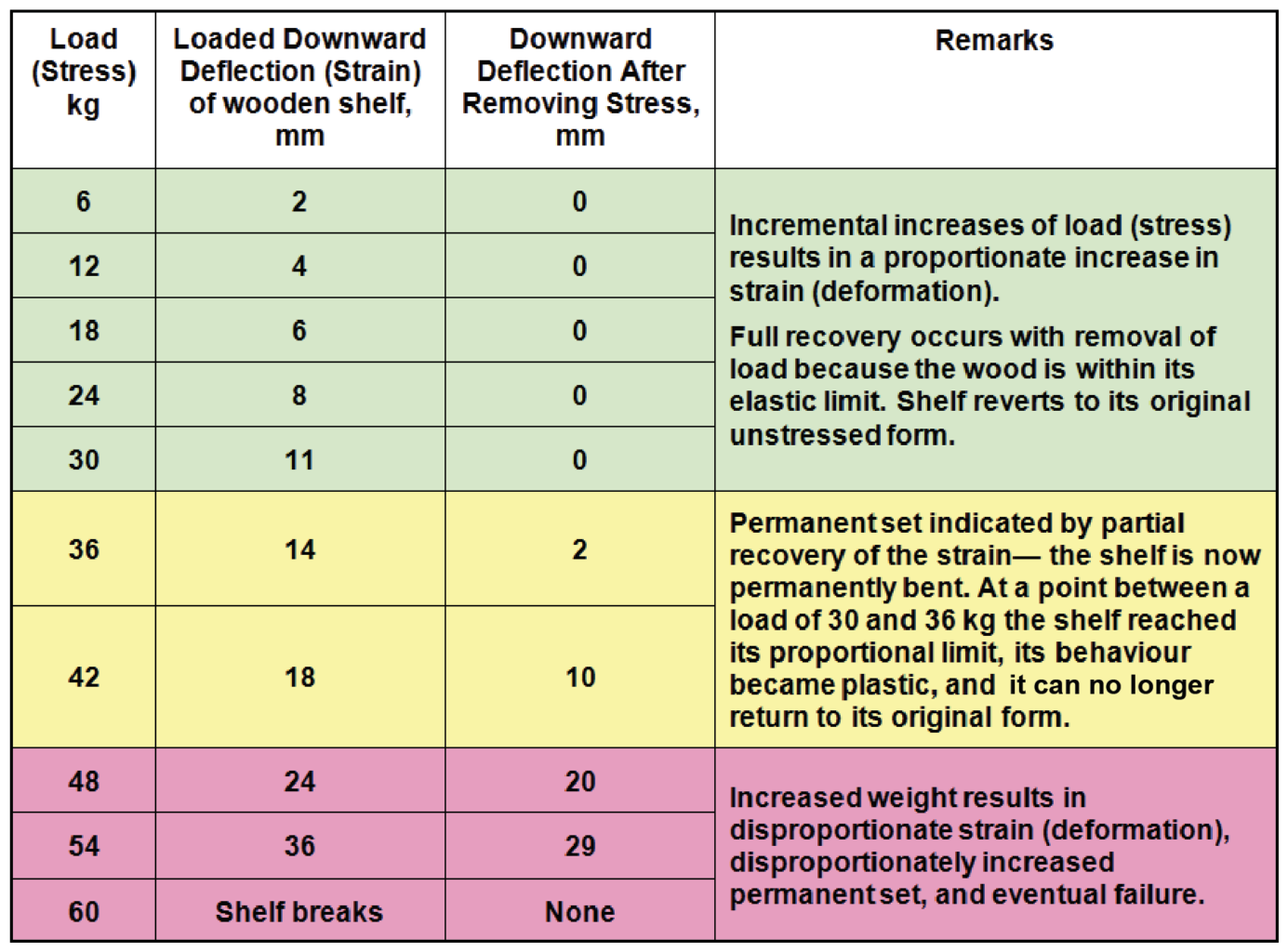
“Hooke’s Law states that the strain is proportional to the stress” (Kollman and Côté Jr., 1968, p 292). Further clarification of Hooke’s Law leads to saying in wood, in common with other materials, stress and strain are proportional up to a particular point. Specifically, that point is the proportional limit. Beyond the proportional limit of the material, increased stress leads to disproportionate strain, i.e., greater deformation, until the material reaches a stage where further stress leads to failure.
Another way of describing this phenomenon is, up to its proportional limit, a material exhibits elastic properties whereby applying a load causes it to deform, and on removing the load the material completely recovers. Beyond the proportional limit of a material, adding bigger loads causes the material to become plastic rather than elastic, and it cannot recover completely after removing the stress and eventually additional load causes the material to fail.
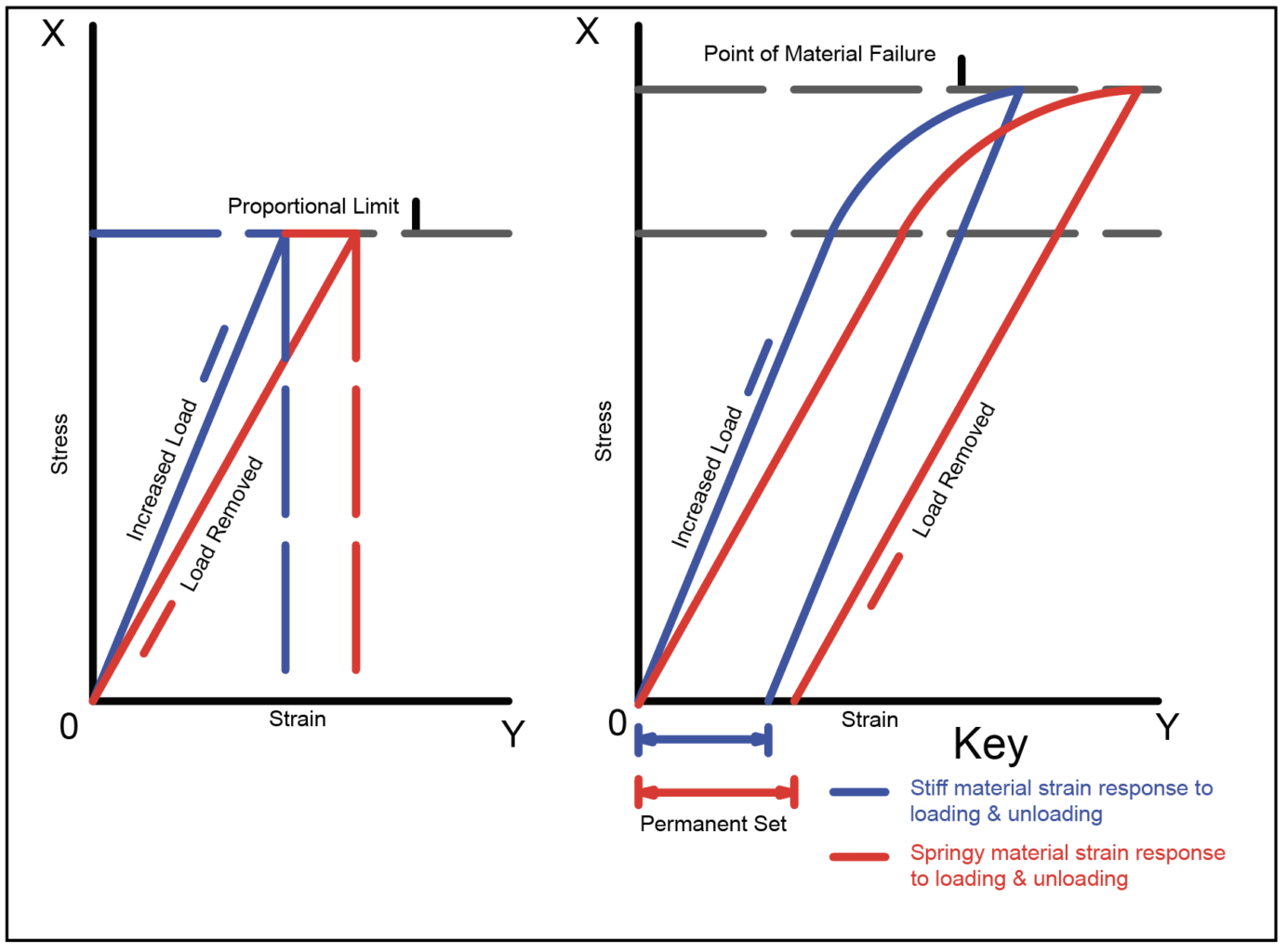
The elasticity of two types of wood, one stiff wood represented by blue lines, and a more flexible one represented by red lines. Generally, stiffer materials are stronger than more flexible ones. Up to the proportional limit, increasing stress (X axis) results in a proportionate increase in strain (Y axis) from which each of the two pieces of wood in this illustration can recover. The slope of the straight-line portion of the graph represents the modulus of elasticity. A steeper line indicates a higher modulus. Stresses above the proportional limit result in greater proportional strain, permanent deformation of the material and permanent set. For instance, a bookshelf loaded beyond its proportional limit takes on a permanent bend. Beyond the proportional limit, the greater the load, the greater is the permanent distortion until the point of failure. In most wood species the proportional limit is generally between 50 percent and 65 percent of load leading to complete failure.
Within the elastic range of a material (up to its proportional limit) the ratio between applied stress and the resultant strain is a constant with this ratio being the modulus of elasticity (MOE), also known as Young’s Modulus. “[It] is a measure of … stiffness or rigidity. For a beam, the modulus of elasticity is a measure of its resistance to deflection” (Forest Products Laboratory, 1955, p 68). Figures 14.18 and 14.19 illustrate the proportional nature of strain in response to added stress where incrementally greater loads act on the centre point of a shelf. This kind of load is a static load.
A rubber band is another item illustrating Hooke’s Law. The law, in the following description, is demonstrated visually rather than measured scientifically. If you hold a rubber band between your fingers and stretch it gently followed by releasing the stress, it will recover its original shape. Successively increasing the strain stretches the band further, and a common visual sign the band is approaching its recoverable limit is increased whitening of the stretched rubber. As the band has to cope with increasing stress it loses the ability to recover and return to its original shape, and further stretching eventually causes the band to break.
The elastic band experienced a tension force that stretched it whereas the previous example, a plank of wood, experienced a compression force through being hit with a hammer head. In both cases the important point is the material experienced a stress (loading) resulting in strain. And in both cases the stress and strain are proportional up to a specific point; beyond that point increased stress leads to greater strain. Stress is a force that can act in more than one direction – stress may in fact occur in multiple directions at the same time, e.g., a part could simultaneously experience compression, tension, and shear stresses (see figure 14.24).
The strength of a material determines its ability to resist stress: an 18 mm- (3/4″-) thick oak book shelf 610 mm (24″) long is significantly stiffer than an MDF shelf of exactly the same dimensions. As a consequence, when both shelves are stressed by loading the same weight at their midpoint, the oak shelf exhibits less strain indicated by less deformation, i.e., it does not bend as much. In addition, the oak shelf is able to carry significantly more weight than the MDF shelf before it fails completely.
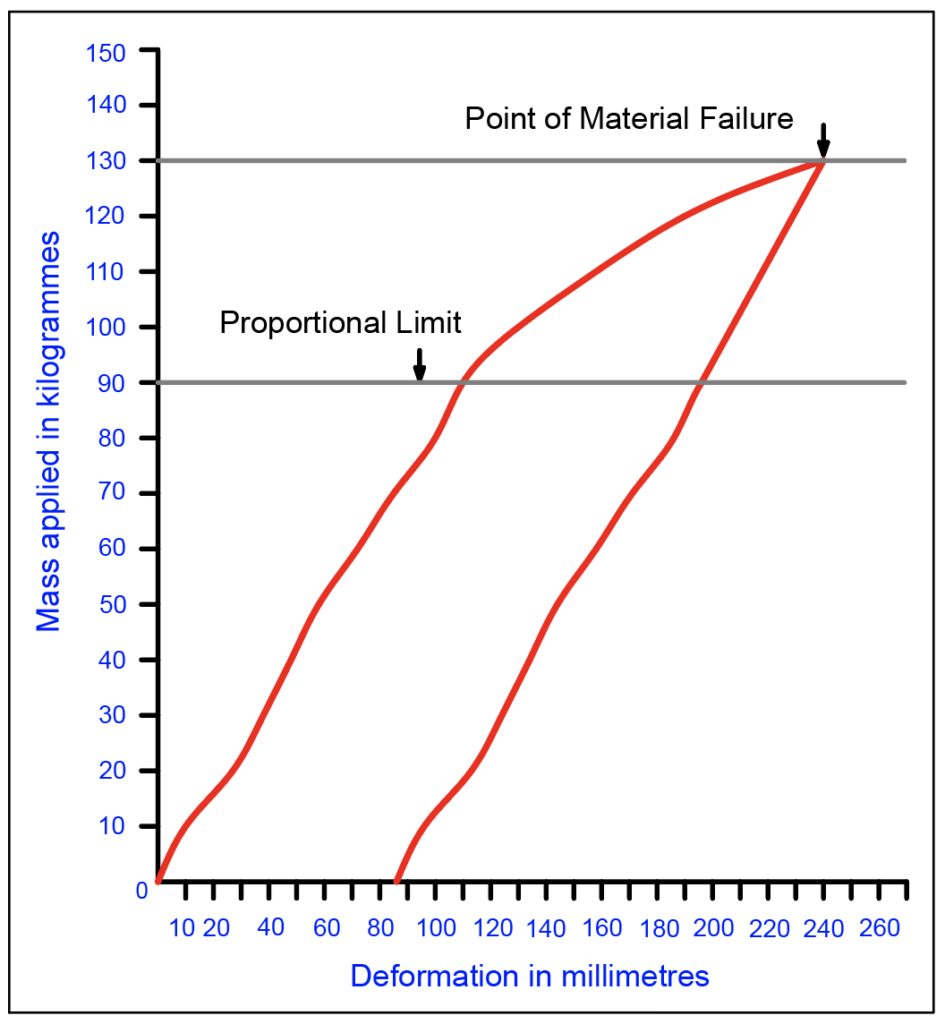
A simple static bending load experiment to demonstrate Hooke’s Law.
Static bending occurs under a constant load or when a load gradually increases. The set-up is a rudimentary partially fixed end beam with a knot-free softwood fence paling (picket) screwed down at both ends to span between the two sawhorses. The distance between the bottom of the paling and the ground was measured and noted. Concrete blocks, each weighing approximately 10 kg, were loaded onto the paling, and the distance between the paling and the ground measured. This was followed by removing the blocks, and a note of the distance between the ground and the paling taken again. The sequence was: Add one block, measure, remove the block and measure again; next, load two blocks, measure, remove the blocks, measure again, etc. The paling recovered to its original condition up to the point where adding and subsequently removing 9 blocks (~90 kg); this was the “proportional limit” of the material. Loading additional blocks led to greater bending of the paling under the load, and ever greater permanent distortion (permanent set) of the paling after removing the load. Complete failure of the paling occurred with a load of 13 blocks (~130 kg). This experiment did not represent true scientific testing; it is evident, for example, the outermost feet of the sawhorses had lifted off the ground in the middle image, which compromises the accuracy of measurements gathered. However, the accompanying graph, figure 14.23 derived from the experiment, illustrates Hooke’s Law reasonably effectively.