See the first installment of this series here.
Note: This entry has been updated to fix an embarrassing geometry mistake. The repaired paragraphs are in italics.
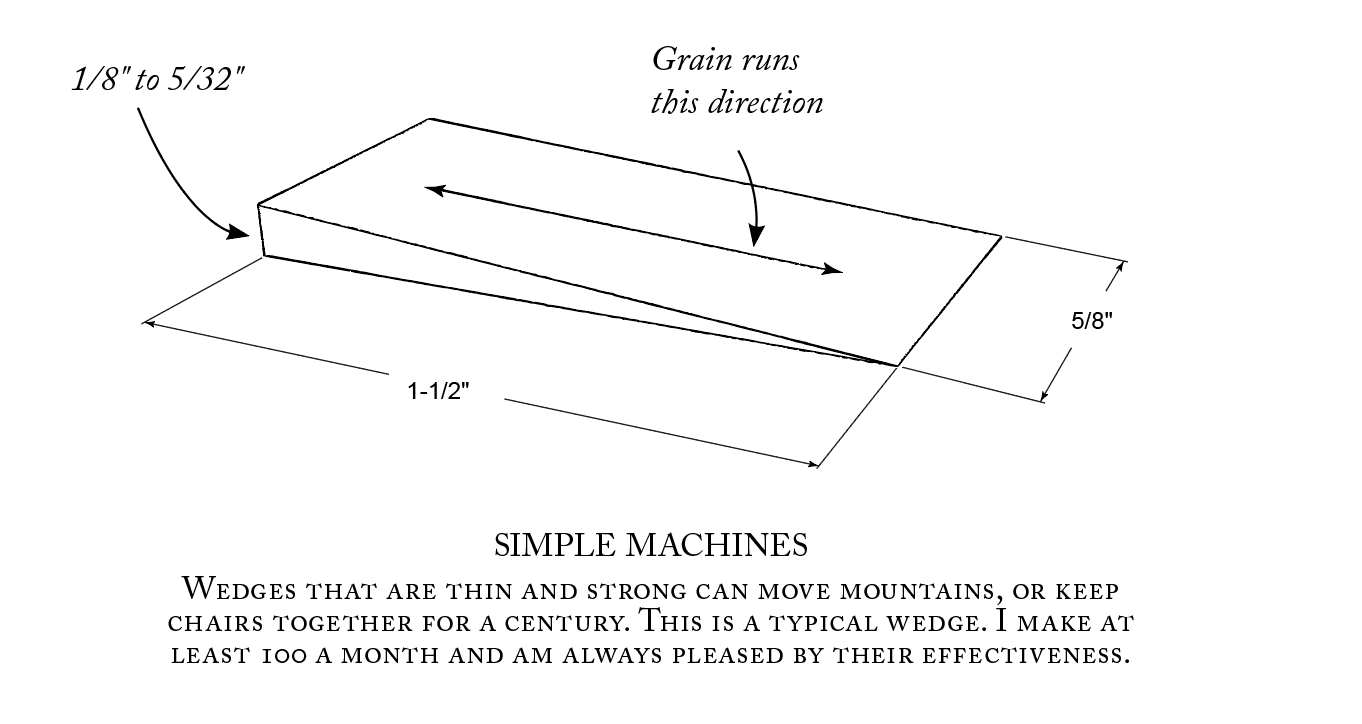
Wedges for stick chairs must absorb a lot of shock so they don’t snap when you install them. So I steer clear of weak (sycamore) or brittle (ebony) woods.
Most of my wedges are oak or ash, species that are plentiful and inexpensive. I don’t think I’ve ever snapped an oak or ash wedge, even when I’ve struck them at odd angles. I have used walnut and cherry wedges at the request of customers. They work, but you have to be deliberate when hammering them in because they will snap.
The grain in a wedge should run along its length, from its thin tip to its fat end. For chairs, I use wedges that are 1-1/2″ long. The fat end is between 1/8″ and 1/4″ thick. The tip comes to a sharp point. If I need a blunt tip for some reason (say the tenon is loose and shallow), I’ll snip off the pointiness.
The angle of the wedges I use is usually somewhere between 4° and 10°. The shallower angles are easier to hammer in, but the wedge is more likely to crack. A wedge with a larger included angle can cause the wedge to bounce out of the tenon when you hammer it in. The solution is either to hit the wedge harder until the wedge hopefully grabs, or switch to a wedge with a smaller included angle.
Wedges with included angles smaller than 4° can work, but the wedge is even more likely to snap off when struck.

Wedges With & Without a Sled
You can make wedges without a jig on the band saw by using the saw’s miter gauge. Crosscut a 5/8″ x 1-1/2″-long chYou can make wedges without a jig on the band saw by using the saw’s miter gauge. Crosscut a 5/8″ x 1-1/2″-long chunk off a board that is about 6″ wide. Set the saw’s miter gauge to cut on-half of the angle you desire (i.e. 5° off 90° for a 10° wedge). Put the chunk on the miter gauge and cut off a thin sliver. Flip the chunk over – end grain-for-end grain. Slide the chunk toward the blade and make another cut.
You will quickly figure out where to place the chunk so that you make a perfect wedge. You can make wedges with thin points and blunt points.
Keep flipping the chunk over and over. Make wedges until your chunk is so small that it feels dangerous to make the cut while so close to the saw’s blade.


You can also make a dedicated wedge jig for the band saw’s miter slot that has zero clearance to the blade. This jig is shown above. It is permanently set at 5° off 90° and makes it easy to position the chunk of wood and slice a perfect 10° wedge.
The disadvantage to both of these miter-gauge methods is also its advantage. The technique makes it easy to make different wedges. By moving the chunk of wood left or right on the miter gauge, you can make wedges that are fatter or skinnier.
— Christopher Schwarz

Looks to me like you are making 10 degree included angle wedges.
Nope. Give it a try and you will see why
The second cut returns the “chunk” to square. Repeat.
Can you define the term “included angle” for the uninitiated? Google doesn’t help a lot
It is the angle inside the tip of the wedge. I’m sure a geometrician can give you a better reason as to why we call it “included angle.”
Google and ye shall find. The bottom line is that an “included” angle is the interior angle formed between two intersecting lines. For us dummies, it’s a plain vanilla inside angle, so I suppose it would have to be 90° or less. Here’s a formal definition. The link below will take you to an illustration.
Definition: The angle made by two lines with a common vertex
Included angle – the angle between two given lines that meet at a point.
When two lines meet at a common point (vertex) the angle between them is called the included angle. The two lines define the angle. So for example in the figure above (see link below for the figure) we could refer to the angle ∠ABC as the “included angle of BA and BC”.
Or we could refer to “BA and BC and their included angle”.
https://www.mathopenref.com/angleincluded.html
I’m missing something, or included angle doesn’t mean what I thought. The first cut from a squared chunk gives me a 5 degree wedge, each subsequent one is 10 degrees. Should the miter gauge be set to half the included angle?
But the end is cut at 5° going the other way. If you try it and measure, I think you will understand why it’s not 10°.
This is confusing, I didn’t mean to post anonymously. My bandsaw isn’t the greatest, but the wedges I cut are about 1/4″ thick at the fat end tapering to zero at 1 1/2″ long. I think I may have misunderstood your method.
I believe it’s an isosceles triangle with a base of 1/8″, so two right triangles with 1/16″ bases back-to-back. The height is 24/16 (1 1/2″). The inverse sin of 1/16 divided by 24/16 is 2.39. That’s the angle of one of the triangles. There are two, so the angle is 4.78°.
Or, if I’m envisioning it wrong and it’s a right triangle, the base is 1/8″ and the height is 12/8. The inverse sin of 1/8 divided by 12/8 is 4.78°.
The difference between the two triangles is at the third decimal place (4.780° vs 4.776°).
For the top angle to be 10° the base would have to be a little over 1/4″.
[Forgive me if this is a duplicate. For some reason my browser doesn’t play nicely with WordPress’ authentication system.]
I didn’t mean to post my geometric explanation anonymously either. Hopefully I’ve figured out my WordPress issue.
Your math seems right to me here, but it seems like your inputs are wrong. If you use this method and then cut a wedge that has a 1/8″ thick base, then the height of the triangle is around 7/8″ +/- when I cut the wedge. The angle doesn’t change whether I cut the base to be 1/8″ or 1/2″ or any other dimension does it since the jig hasn’t changed?
You got it right. The first wedge cut from a squared board will be a right triangle. That’s why the first one gets tossed. Each subsequent wedge will be an isosceles triangle, just as you describe.
Yes exactly, although strictly speaking I think one should use inverse tan rather than sin. At these angles and application there is no significant difference. Apologies for sounding pedantic. Or maybe obtuse. (sorry!) But as I (mis?)understand the method, each of the isosceles wedges ends up being essentially two of the initial right triangle wedge stuck back to back, doubling the included angle. Which is what I found when I tried it out: the first one has a ~1/8″ base while the next ones are ~1/4″.
I fear that I, too, must join the rank of the confused! I will not try my hand at trigonometry (which I was taught at school, 40 years ago, and promptly forgot all about), but unless I’m much mistaken, a basic tenet of (Euclidian) geometry is that the sum of the internal angles of any triangle is 180º. So, if I set my miter gauge to 5º, and then follow the instructions above, after the initial right angled triangle-shaped cut, I will produce a series of isoceles triangle-shaped wedges, where both external angles at the base (the blunt end) are 5º of 90º, and the corresponding internal angles thus 85º. As 85º + 85º = 170º, the internal angle at the tip (the thin end of the wedge) must be 10º.
In practice, this is also what I get and can measure. I tried the method as described, and found the external angles at the base to be 5º each, and the internal angle at the tip to be 10º (or as close as makes no difference). Furthermore, with the total length of the wedge at 1-1/2″, the base was not 1/8 to 5/32″ thick, but more or less the double — on the wedge that I measured it came in at 9/32″.
In other words, I think that with the basic measurements as given in the blogpost of an isoceles triangle-shaped wedge 1-1/2″ long with a +/- 1/8″ fat base, the wedge will indeed have an included angle at the tip of about 5º.
However, unless I have either misunderstood (and mis-reproduced) the method, or am otherwise being obtuse (to be fair, either or both of which are very much within the realm of the possible), it seems to me that the miter gauge should be set to 2.5º in order to produce the desired 5º included angle wedges?!
Cheers,
Mattias
By-the-by, I forgot to say that I’ve been using a similar method on my Byrnes Model Machines miniature table saw, only with two miter gauges, each set to 2º off of 90º, but in opposite directions, thereby eliminating the need to roll the blank over, thereby eliminating the need for both crosscut edges of the blank to be parallel to each other, as all cuts are referenced off of just one of them.
I just went down and measured one of the wedges I’d previously made this way. The included angle is indeed 4º, and at 1-1/2″ length, the base is about 5/64″ thick.
Cheers,
Mattias
I must not understand the directions and am doing something incorrectly. I measured the second wedge (and any subsequent wedges) and I get 10 degrees.
Nice wedges. Ten degrees.
Chris I thought you had a different jig to cut wedges for the chairs.
Chris,
I’m sorry to keep banging on about this blogpost, but it just won’t stop bothering me. In particular the illustrations look as though they might be from your upcoming stick chair book, and I just can’t square what they, and the text, say about setting the bandsaw miter gauge (or wedge-making jig) to 5º, with producing isosceles wedges that have an included angle at the tip of also 5º. I have tried approaching it with math, by sketching it out in Illustrator, and by making wedges on the bandsaw, and the results are consistently the same: two 5º saw cuts referenced from alternating end-grain edges give me isosceles wedges with an included angle of 10º at the tip and, at 1-1/2″ long, with a blunt end that is about 1/4″ thick.
To my mind, this means one of two things: either I’m making a stupid mistake somewhere along the line, or your instructions to set the miter gauge to 5º are wrong. I’d be delighted for it to be the former, but am worried that it might be the latter, and that you are about to have that error printed.
You are quite right. None of my dang business.
Nevertheless.
This is how I’ve understood the method you describe:
You crosscut a blank as wide as you want the wedges to be long, for example 1-1/2″. Thickness and length of the blank does not matter for the angle question, so let’s leave them out of the equation here.
This blank has two long edges, parallel to each other, both of which show end grain. Let’s call them E1 and E2.
The miter gauge is set to 5º off square, i.e. 5º off the setting that would give a square crosscut (“0″ on my bandsaw miter gauge). Whether to the left or to the right does not matter.
The blank is held with E1 against the miter gauge fence, and E2 facing into the saw blade, and it’s outermost left end pushed through the saw. The cut-off is discarded.
The left end of the blank now is now no longer square (or however it started out) but biased, relative to both E1 and E2, at an angle of 5º, again both relative to E1 and to E2. These two 5º angles are of course in opposite directions, and depending on how you measure them, you could also say that one is at 85º and the other at 95º. No matter. It means the same thing.
Now, the blank is rolled over through it’s longitudinal axle, so that E2 is held against the miter gauge fence, and E1 faces the saw blade, or as you put it: flipped end-grain for end-grain, and then slid to the left just enough that the next cut produces a wedge-shaped cut-off with a tip thin (or fat) enough to suit your purpose. Again, the blank is left with a biased left end, 5º off E1 and 5º the other way off E2.
Then, flip again, so that E1 sits against the fence and E2 faces the saw, slide to the left, and cut; flip, slide, cut; flip, slide, cut; and so on until you run out of blank length.
If I do this with the miter gauge set to 5º, I get isosceles wedges where the included (i.e. internal) angles between the short base line at the blunt end and either leg are 85º, and the included angle between the two legs at the tip is 10º. And if the legs are 1-1/2″ long, the base line is about 1/4″ in rounded-off numbers.
If on the other hand I set the miter gauge to 2.5º, and for the rest do everything as described above, the included angle at the tip is 5º, and with 1-1/2″ legs, the base line is about 1/8”, which are the measurements you give for these particular wedges.
If (as is very likely) I have misunderstood something, it would of course be great if you were able to point out the error of my ways to me. However, if you have better things to do (and I would be rather surprised if you don’t), please just call me a cab (“hey, you’re a cab!”), and leave it at that.
If, however, it seems to you that I have not misapplied your method, and if those illustrations are indeed from the upcoming book, you might perhaps just want to double check those miter gauge/wedge jig angle numbers before the printers have had time time to apply ink to paper?!?
Cheers,
Mattias
Hi Mattias,
We are swamped in getting ready to open for classes (prepping stock for seven full-size tool chests) and getting the Dick Pronneke book to press. So I haven’t had time to sit down and read all the comments. I will. I’m not trying to dodge a potential mistake. It’s just not my highest priority, and there are only so many hours of the day I can devote to arguing on the internet.
All best,
c
Hi Mattias,
I finally had time to go back and figure out where I went wrong. I’m not sure how I got turned around, but I did. The post above has been corrected reflect the error and the fix will appear in the second printing of “The Stick Chair Book.” Sorry for the delay in repairing things. We have been insanely busy with our first post-pandemic class and two books. Thanks for staying on my butt about it!