 English oak coffer; 16th century. (Image from Wiki Commons, public domain.)
English oak coffer; 16th century. (Image from Wiki Commons, public domain.)
The once ubiquitous coffer (from the Greek “kophinos” – a basket; later from the French “coffre” – a chest) was also referred to as a “strong box” – because it was. (Later the term coffer would refer to an institution’s financial reserves.) This stout, often highly ornamented, chest reached its pinnacle of design and construction in the mid 1600s and was likely the first, and perhaps the only, piece of furniture that a commoner family might own. Likely used every day as a bench, its primary purpose was to keep the family’s valuables safe and private. Its thick oak walls and lid could often even keep its contents safe from a fire.
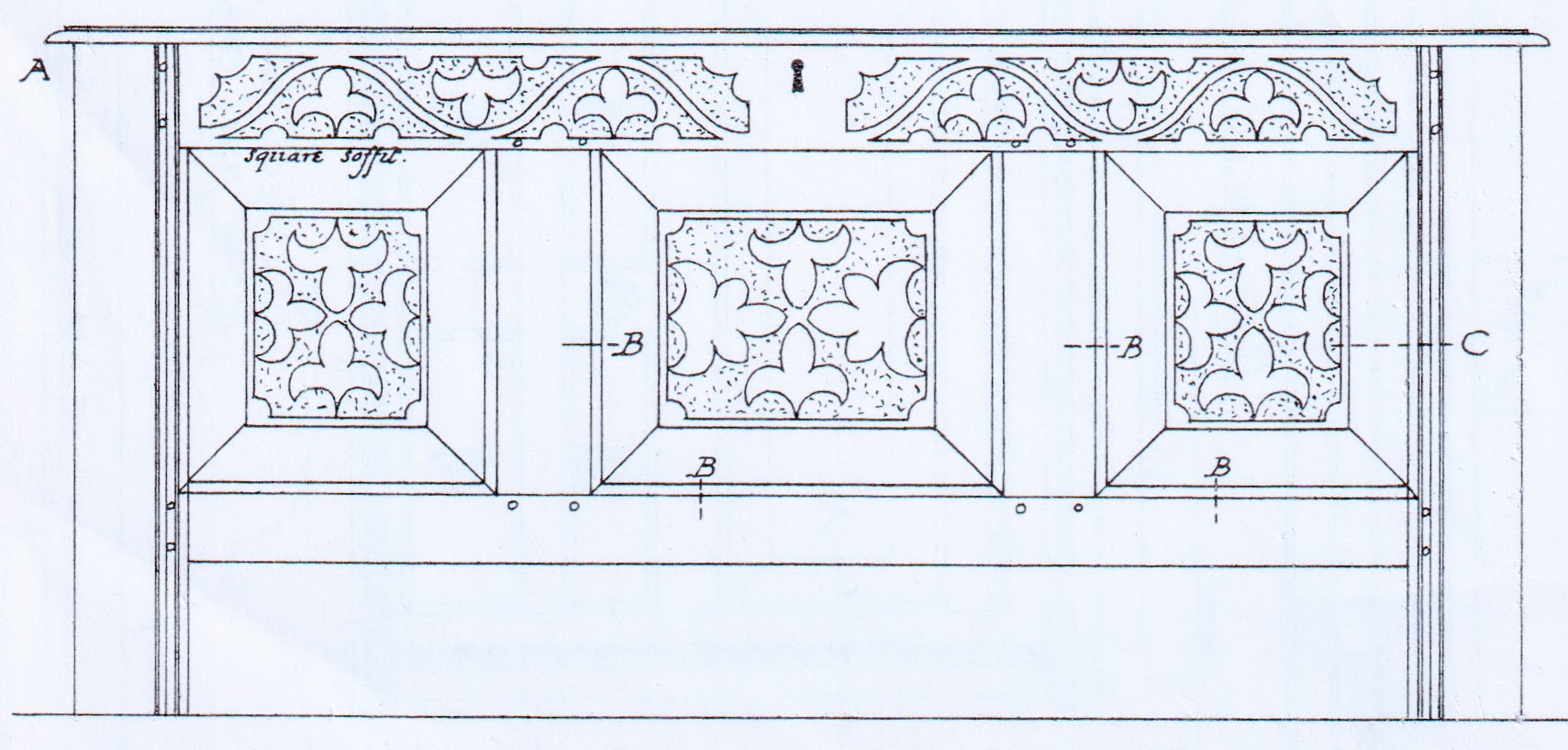
 Accurate drawing of a similar 17th century English chest (by John Hurrell, published in 1903).
Accurate drawing of a similar 17th century English chest (by John Hurrell, published in 1903).
For George Walker and me, what is truly fascinating about these coffers is that they clearly demonstrate the traditional, artisan design process we have described in excruciating detail in “By Hand and Eye” (and decidedly less excruciatingly in “By Hound and Eye”).
For those unfamiliar with this process, here it is in a nutshell: Unlike modern builders who think primarily in terms of measurements to an external standard such as inches or centimeters, pre-industrial artisans took their cues from the builders of antiquity and thought more in terms of proportions. They would start by selecting a simple rectangle of harmonic proportions (literally from the audible harmonic musical scale) to govern the overall form. For example, the front elevation of height-to-length were commonly ratioed at 1:2 (an octave); 2:3 (a perfect fifth); 3:4 (a perfect fourth) or 3:5 (a perfect sixth). Within this rectangle they would select the span of some prominent element of the structure to act as a module (an internal index measurement often based on a element of the human body) and then tie all the other details proportionally to it.
The coffer is a perfect example of this ancient design process: a straightforward layout based on the geometry of a cuboid defined by simple whole number ratios of height, width and depth. Like the proportions embedded in the design of Grecian columns (which deeply influenced the design methodology of the joiners and cabinetmakers of the 17th and 18th centuries) the designer of this coffer clearly used the width of the chest’s leg in the front elevation as the “module” for the design. (The Greeks used the diameter of the base of a support column’s shaft, which happens to be the span of the human body, as the module for all the other elements of the temple.) We encourage you to print out the above drawing by Hurrell, take a sharp pair of dividers, set it to span the width of the leg (we label it “M”) and go exploring with us:
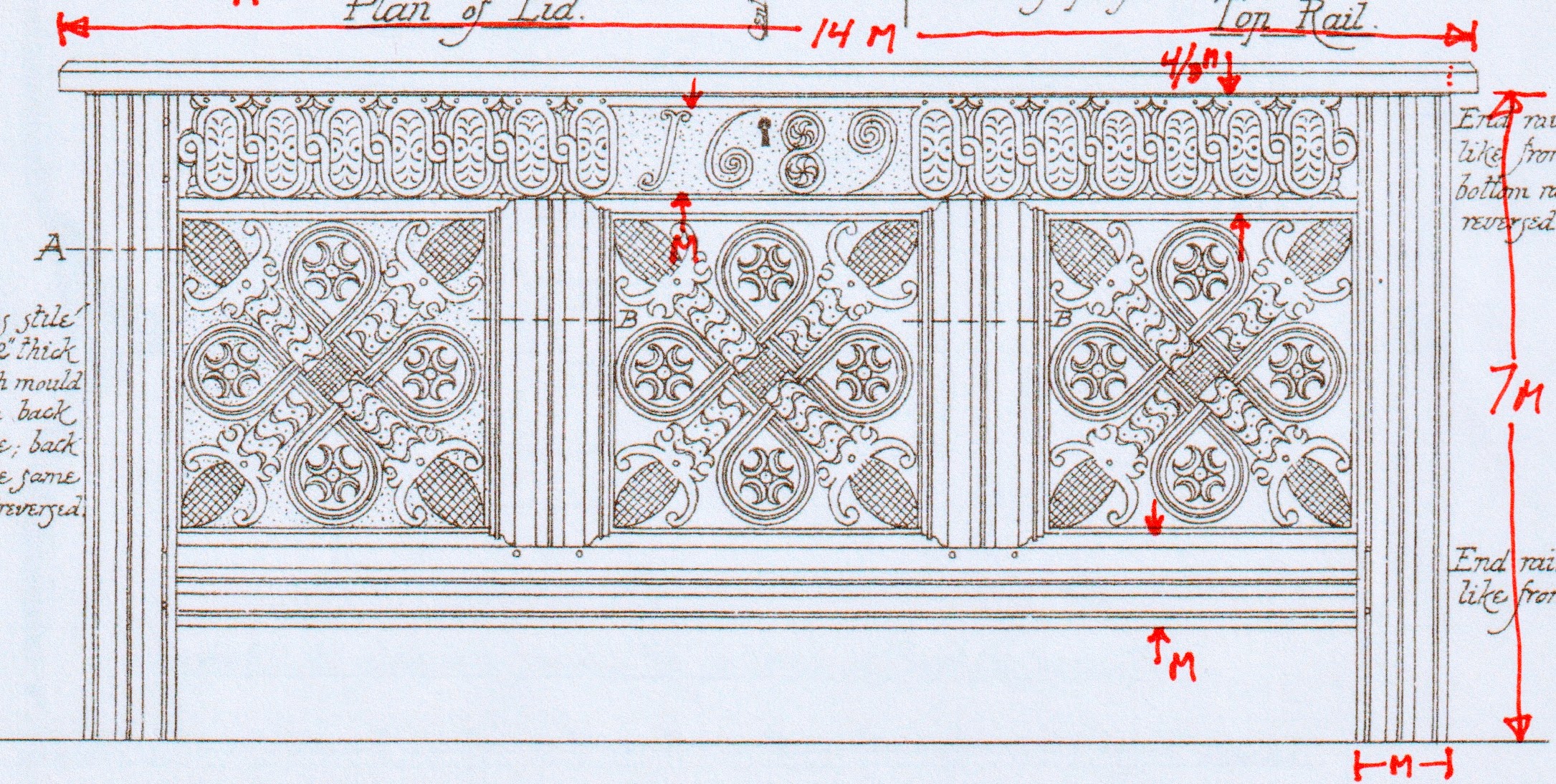
The first thing we’ll discover is that the height of the leg (to the underside of the lid) is exactly seven times its width (again, the module for this design). By eye, it looks like the length of the chest may be twice its height. When we step the module between the outside of the legs, however, we don’t come up with that nice whole-number ratio. On our second shot at it, we discover the lid from edge to edge is a precise 14 modules long. So there’s our 7:14 ratio – or to simplify 1:2. Which is a perfect octave harmonic, and a common choice for the coffers of this era (and later for highboys in their vertical extension).
Further exploration reveals that the mid-stiles and bottom rail are also a module wide, as is the height of the carved inscription of the date 1689. If you continue poking around, you’ll unearth all manner of modular-indexed relationships buried in the intricate geometric carvings. Be aware that the spans and radii, if not exactly a module-length, will be a whole number fraction above or below that length. For example, the module (plus a third of the module) serves as the spacing for the positioning of the lower rail from the baseline as well as the width of the top rail.
As in the ancient temples of Greece, every single element of this coffer enjoys a whole-number relationship with each other – and with the overall geometric form. As such, you can scale this piece of furniture up or down by simple changing the span of the module – no measuring to numerical dimensions is necessary – just an adherence to the ratios.
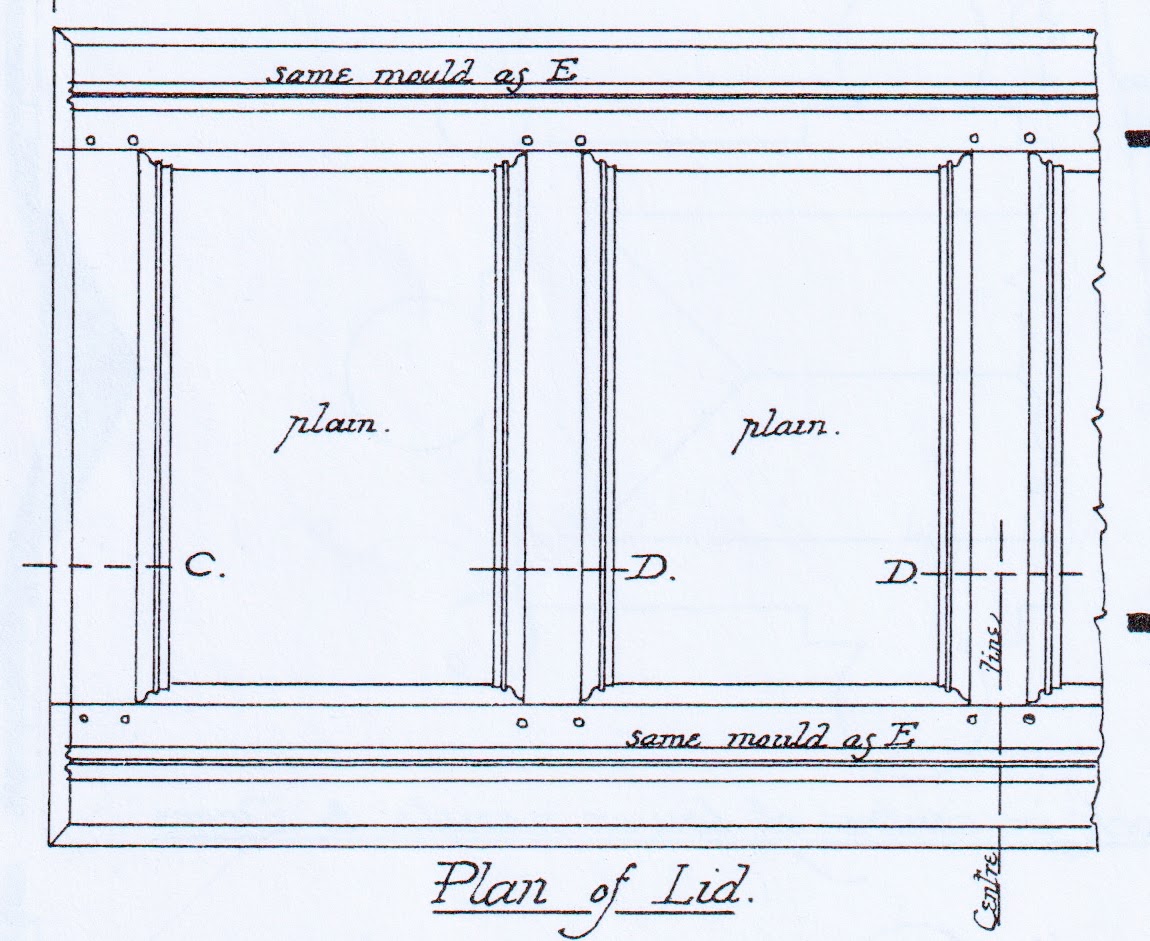
Now let’s explore the design of this coffer’s frame-and-panel lid. We were excited to discover how some anonymous 17th-century artisan made clever use of the module to add subtle, eye-pleasing asymmetry to the layout. Before you see how they did it (below), try to discover it for yourself. We find this sort of thing fun, and we bet you will too.
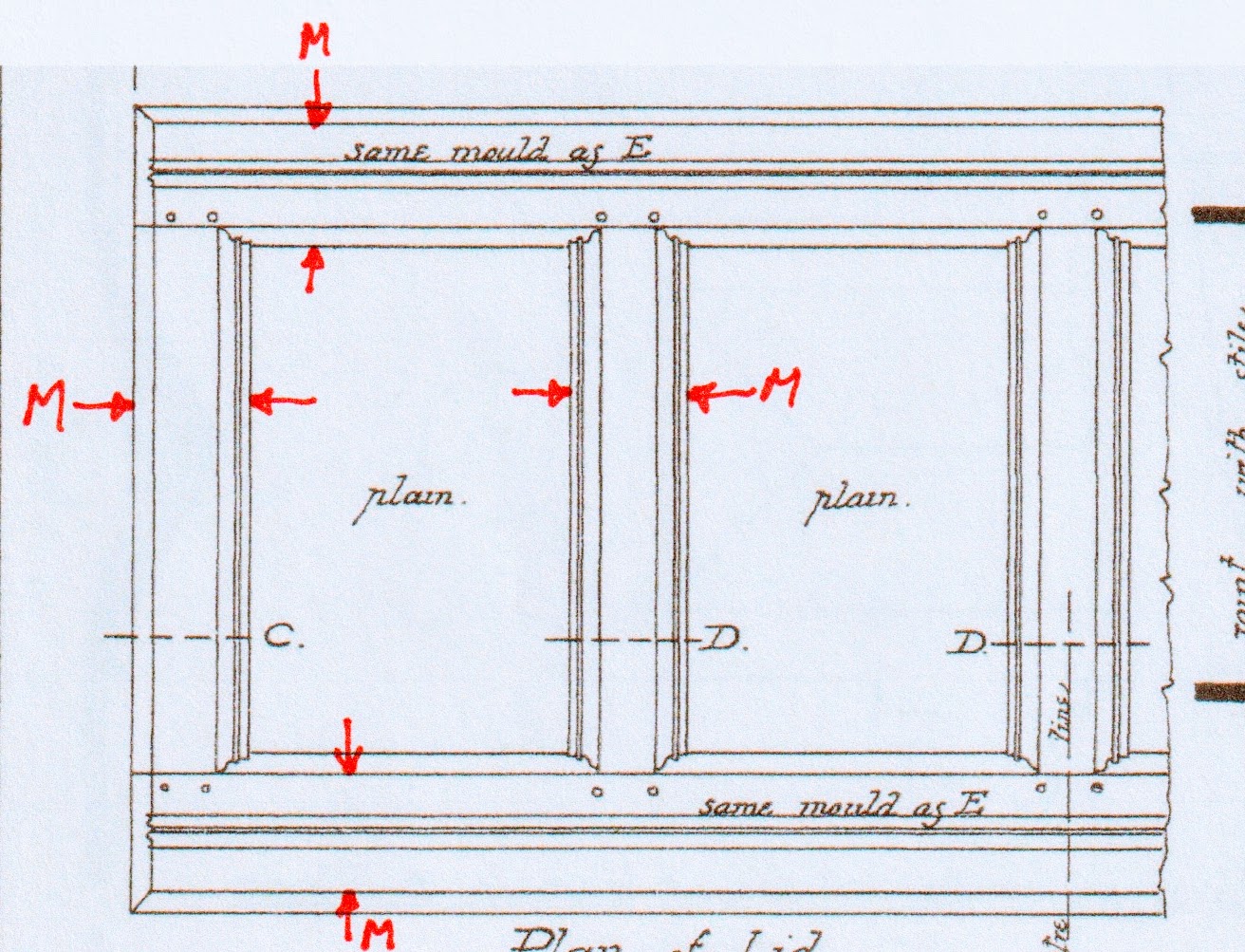
So here’s what we found: The module is utilized in four different ways: For the middle frames, it defines its overall width; for the hinge-side frame it defines its width, but it does not include the lid edging; for the end frame it does include the edging; and for the latch-side frame the module defines its width from the inside of the edging to the edge of the bevel next to the panel. Subtle, but just enough to make the design lively to the eye.
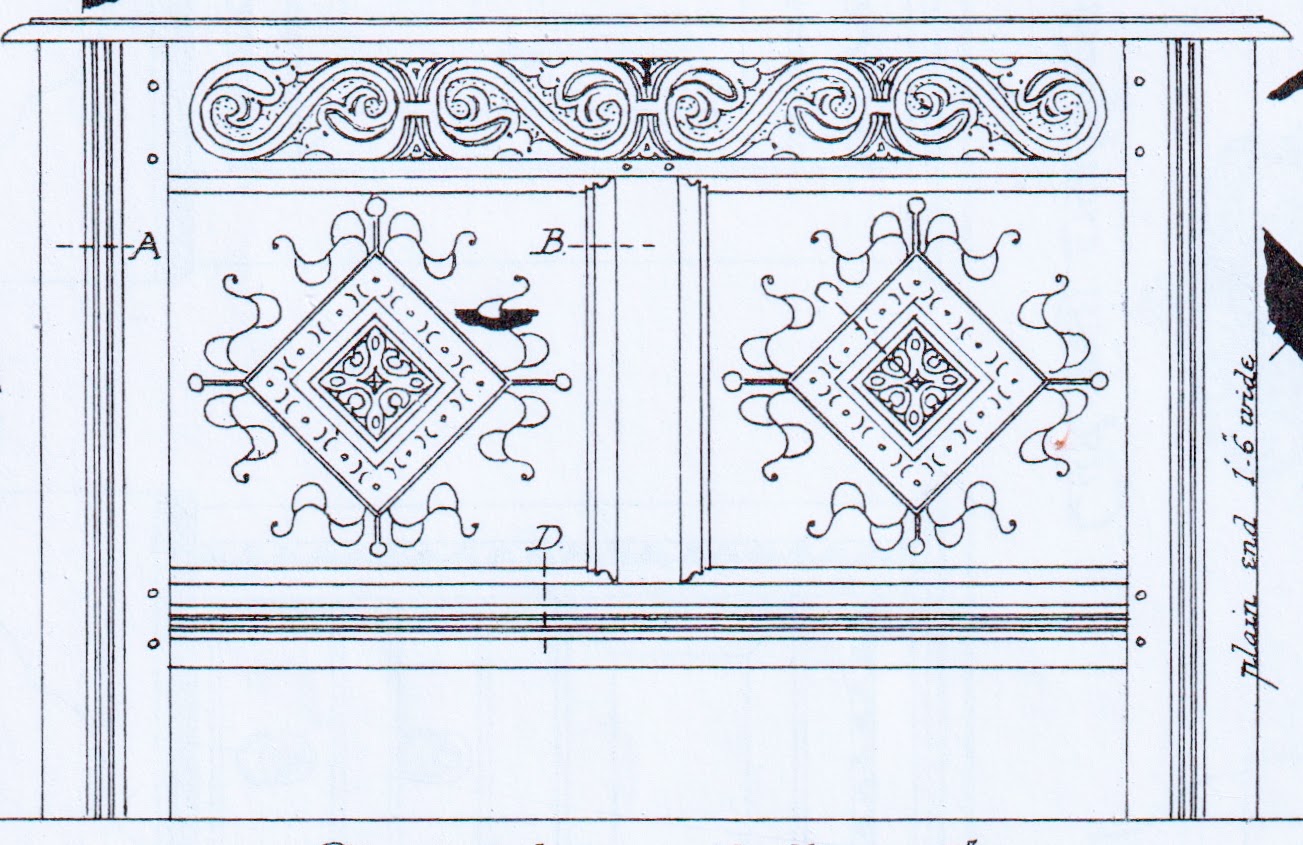
For your further entertainment, below are a couple more of Hurrell’s drawings of 17th-century English coffers for you to print out and explore. To see what we unpacked with our dividers, check out our blog at www.byhandandeye.com. One hint/reminder: The module for each of these designs is the width of the leg.
To learn more about the construction and carved ornamentation of these traditional coffers (also called a “joined chest” in America), you can do no better than to watch Peter Follensbee’s video “Joined Chest” available from Lie-Nielsen here or to read “The Artisan of Ipswich” by Robert Tarule, available from John Hopkins University Press here.
— Jim Tolpin

I hate to be that guy, but 6ths are major or minor, not perfect. 3:5 is a major 6th. Great post!
We stand corrected Steve…thanks for the clarification.
Very interesting article.
And it’s making me squirm a little,” but for next time it’s… “For George Walker and me….”
Beautiful post about a classic and captivating subject! Do you not have one of your own that you could photograph? Clearly not an easy DIY here.
We need to be careful with any proportional analysis like this, especially since we aren’t looking at the original object. First of all although Hurrell’s drawings are supposedly measured drawings, he or whoever actually made the drawings was almost certainly trained in a tradition that told him to look for simple proportions in order to simplify his sketching. The results are very likely to be idealized versions of what was actually observed and aren’t likely to be especially reliable.
That said, I think it’s most probable that the module as such is derived from the square panels with the leg width being about 1/3 of the panel width.
The panel decoration is based on a pattern of circles in a cross configuration of 3 circles tall by 3 circles wide. (3×3 grid, omit 4 corner circles leaving 5)
Another circle shares a center with each of those remaining 5 with a radius equal to 2/3 of the radius of its outer circle. Those define the inner circular lines of the strapwork with the one in the center defining the 45 degree square.
If a circle is drawn around the whole group (3 module diameter with origin on panel center), then the center smaller circle (2/3 radius) copied to the upper right at 45 degrees will fit tangent to the outer circle and the top and right circles of the original group of 5. The same is obviously true for the other corners too.
The 2 center stiles are 2 of the smaller circles in width. That’s also equal to 1 1/3 of the original “module” circle or that circle’s diameter plus the difference in the two.
The 1/6 division of the module circle’s diameter (from which the 2/3 radius is derived) also seems to be the basis of the horizontal spacing of the elements of the carving on the upper rail. The space below the bottom rail is 1 1/6 of the module circle. The top is about 2/6 thick as is the overhang of the top past the box
Jenohdit: Thanks for contributing your further analysis of the coffer. I would suggest that whoever built this piece was also steeped in the ancient tradition of building to simple proportional relationships. I’ve also observed that historical pieces often deviated a bit from being perfect representations of those proportions—likely due to the typical building process which often requires a fudge factor to trim certain elements to fit.
I agree with being carful on proportional analysis, in particular when it comes to actual objects. When I planned my wall cabinet, I based it upon a module of 3 inches. One night, while attempting to get out of the shop in time for dinner, I nailed and glued the sides/stiles ( no rails ) of the face. I was the next day I realized that I had neglected to rip the stock from 3 1/2 to 3. Rather than fuss with removing them, i just repeated the mistake on the rails and stiles of the doors. My drawings of the cabinet are in proportion, the cabinet itself is not.
John Hurrell was almost certainly the only person who ever drew that chest. The drawing may or may not be accurate. He had a Victorian eye.
One of the most interesting pairing of objects I have ever seen was in an exhibit called Pompeii and the Roman Villa at the National Gallery of Art. There was an original marble table base from the House of Gaius Cornelius Rufus and a Victorian copy as well as a painting by Sir Lawrence Alma-Tadema called “a Sculpture gallery” which depicted it.
It’s hard to describe the differences but they were striking. The original was loosely laid out and none of the repeated elements was identical nor was anything actually symmetrical. The Victorian copy was perfectly repeated, rigidly symmetrical and looked dead in comparison. The same can be seen in work by Wedgewood or John Flaxman in comparison with Greek or Roman originals. The neo-classicists and later the Victorians were schooled in the idea that there were actual standards for classical orders and that perfect symmetry mattered when the ancients weren’t bothered by that foolishness. See “Ancient Greek Architects at Work” for more on that.
In short, be skeptical of drawing any conclusion from a drawing or a copy of anything. It says much more about the era and sensibilities of the recorder or replicator than about the maker.
I believe the Pompeii table base was frequently copied. Here’s one example
https://www.skinnerinc.com/auctions/2835B/lots/163
Photos don’t do it justice but I found one of the original.
https://p7.storage.canalblog.com/73/27/577050/39000238.jpg
The Alma-Tadema painting is easy to find online.
This is a fascinating post. The lesson I glean from it is that using a measurement of one of the design elements as a base to determine all the dimensions of a project has merit and is a worthwhile consideration for any project….back then or now.