
There are a number of geometric constructions that allow us to create regular (i.e equal-angle and equal-facet length) polygons. Most of those for squares, rectangles and triangles are quite straightforward, requiring but a few steps. However, those dealing with five or more sided polygons get quite tedious involving numerous exacting steps.
Traditional artisan’s constructions are far simpler and each work in the same way to create polygons of any number of sides. The caveat is that they do not generate perfect vertices and therefore do not form regular polygons – i.e. they are approximations. Their products are so close, however, that we cannot see the difference in most drawing and furniture-scale applications. In constructions such as building foundations or landscape layouts, the deviation is a bit more evident. The constructions can, however, easily be “tuned” to near perfect by making small adjustments in the step-out procedures. Here’s a look at three trade-practice methods to create a seven-sided “heptagon.” More details and full instructions for executing these methods are available as a download (free for the next 10 days) at our www.byhandandeye.com shop page.
We use this construction when we know the length of one of the facets of the polygon we wish to generate. Basically, it gives us the focal point of the inscribing circle:
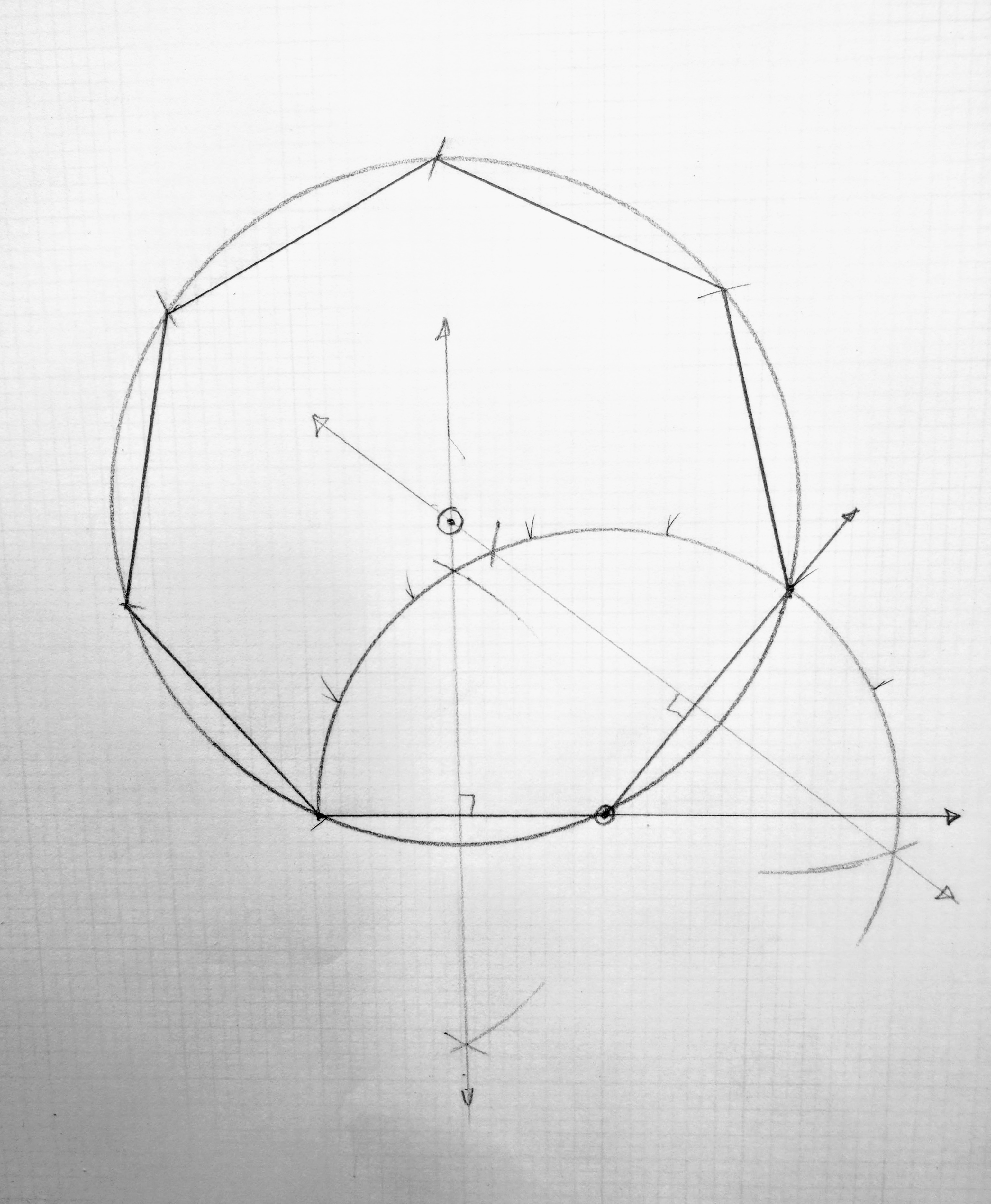
We use this next construction when we know the radius of the inscribing circle. In both of these methods, we are segmenting a line into the number of facets required by our polygon. (In the first, we are segmenting a half-circle circumference line, in the one below, the diameter):
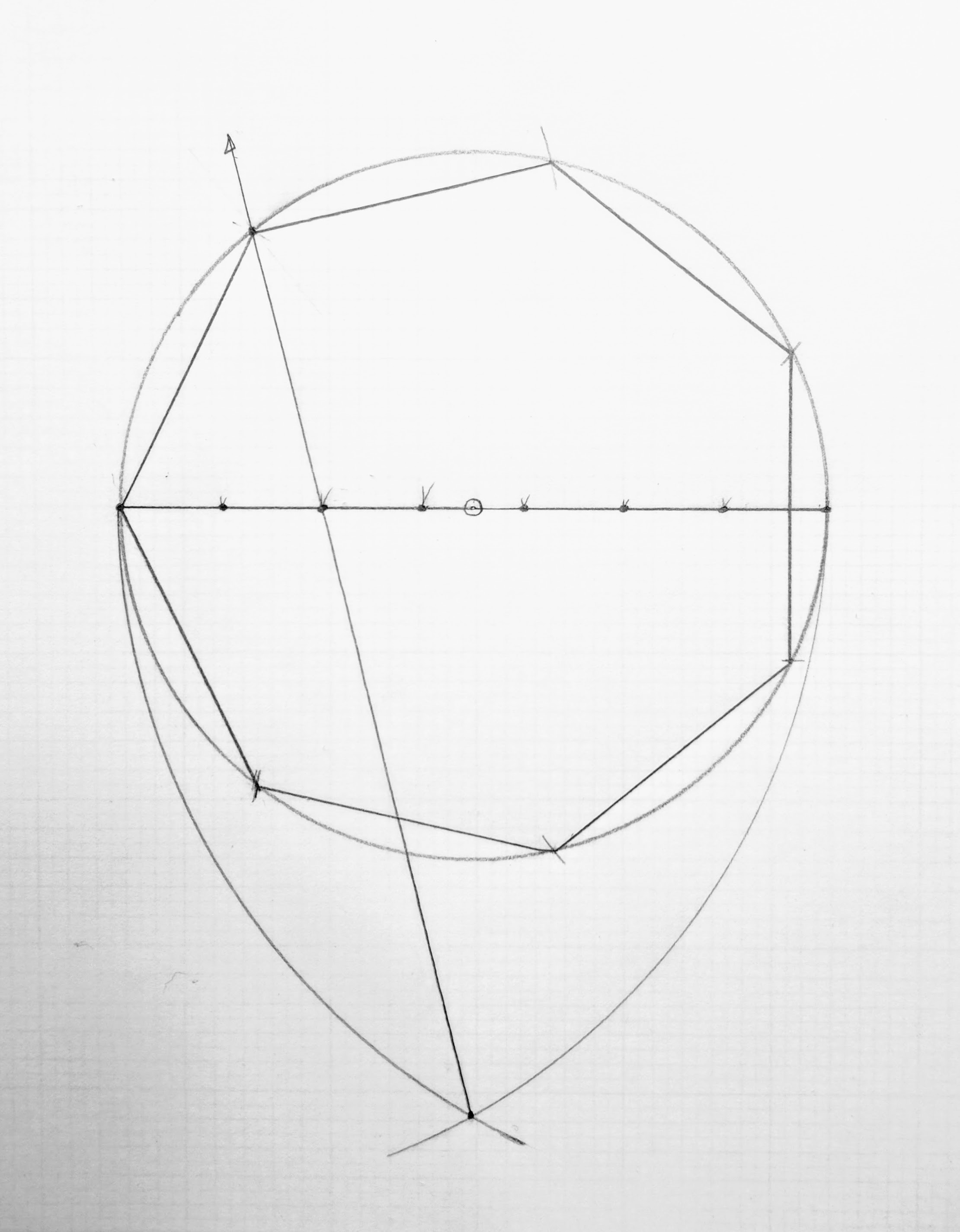
The fastest method, however, is attained through the use of the sector (which you can download for free in the form of a paper template at www.byhandandeye.com).
Using the “line of polygons” (which we derived from another traditional calculator called a “scale of chords”) we start by setting the dividers to the radius of the inscribing circle at the line’s “6” index point:

Then we reset the dividers to the number of facets we want – in this case at “7” for producing our heptagon:

When we step this span around the circle, we have our construction. Again, because this is just an approximation, we will likely have to make a tiny adjustment to allow the dividers to return to the exact starting point. Be assured, though, that you will be so deep in the ballpark with any of these traditional methods that you’ll be able to smell the hot dogs.
— Jim Tolpin, byhandandeye.com

The second method (circumscribed, not inscribed btw) is simple to do by just stepping off as many divisions as you might like around the circle just as you would for a line. If you want a heptagon, start by estimating 8 divisions and then adjust the compass wider until it’s right.
Hexagon is even easier to judge since the facets are equal to the radius–which you have already set on the compass. Since trail and error step outs work just fine, it does make me wonder how often they used these tradesman’s geometry tricks. In large scale layouts for foundations and garden landscapes, perhaps the constructions get you in the ballpark more quickly.
Very good. This discussion is correct in particular when you say:
The caveat is that they do not generate perfect vertices and therefore do not form regular polygons – i.e. they are approximations. Their products are so close, however, that we cannot see the difference in most drawing and furniture-scale applications. In constructions such as building foundations or landscape layouts, the deviation is a bit more evident.
And although implicit in what you say. Let me point out that the error is magnified when he scale is increased. Fortunately circumference is linear with respect to radius so if your error is 0.01 inches in the drawing and your scale is 1 inch = 1 foot , then your error will be 0.12 inches, about the width of two saw kerfs.
Good point Donald. I do find these geo-tricks get you very close in most cases, even in larger layouts.