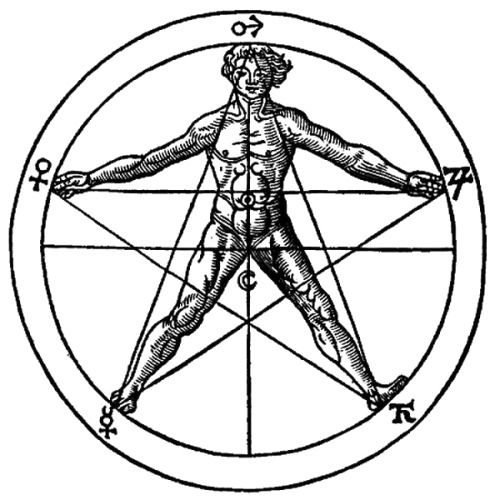
Among Renaissance-era artists, man was often framed within geometric shapes, most commonly (and most famously) squares and circles. However, humans are five vertex creatures (as are the majority of living organisms), a fact that perhaps lead other artists to depict man set within a circle divided into five equal parts: in other words, describing a pentagram. As shown in the mid-16th century illustration above, this artist envisioned man embracing all the quintessential (i.e. five essence) elements, including what later became known in Hollywood as the “force.” The symbols, starting at top and moving clockwise represent: spirit, water, fire, earth and air.

Albrecht Durer, one of the most famous geometer/artists of the Renaissance, developed a geometric construction that generated a five-sided polygon out of the interaction of a certain combination of circles with a square. Symbolically speaking, that exercise would be nothing less than the melding of the triadic cosmos with the earth, the home of man.
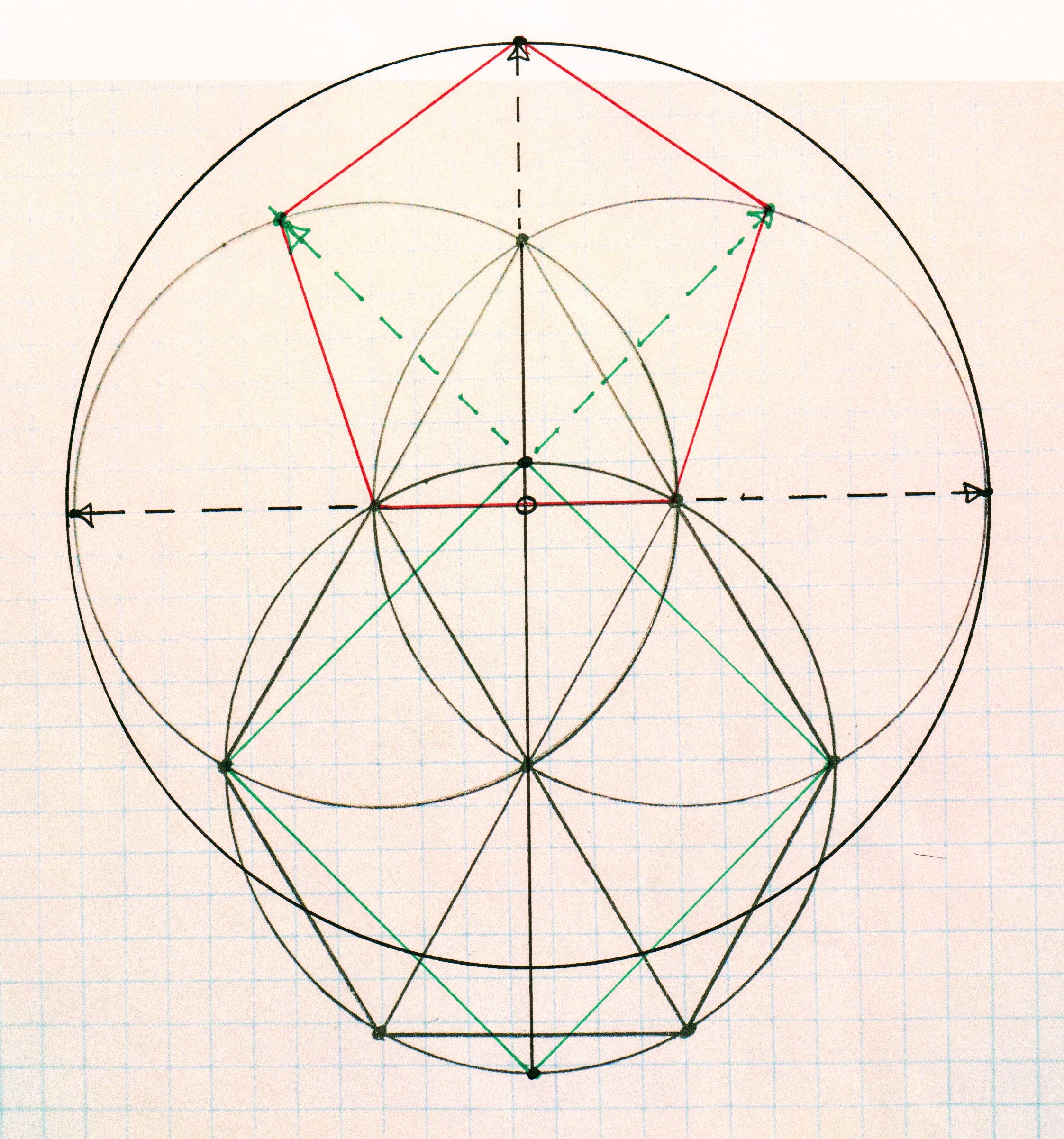
Durer’s construction – the pentagon is in red.
The free downloadable pamphlet we’ve made available here presents the sequence of steps that takes us all the way from a dimensionless point to a pentagon. As we go along, we see how Albrecht’s construction generates the necessary sequence of geometric shapes (circles, triangles, hexagon and square) to get us there. We’ll briefly describe some of the symbolism behind each of the construction phases and then, finally, take a look at whether or not this whole thing is, in mathematical truth, “real.” At that point it’s up to you to decide if any of this symbolic understory has anything at all to do with the design and layout work of artisans (which we have explored at length in our books “By Hand and Eye” and “From Truths to Tools.”) In our opinion: Probably nothing, but possibly everything!
— Jim Tolpin, byhandandeye.com

I get “Internal Server Error”
I’ll check with our webmaster on this issue asap.
Same thing happened to me…Just try again…It worked the 3rd time just fine…
Sometimes its too much for the server if volume is high (I’ve been told…not my world)…
Thanks Jim for providing these…
j
Maybe it’s the Cosmos telling you something…
Please don’t go and open up any alien worm holes or anything…..
Hi, tried to download the said pamphlet but can not. I am taken to your store and add it to the basket for zero cost. When I then try to check out I’m informed you do not ship to the UK. This is strange in a couple of ways.
A, It’s a free download as such doesn’t need to be shipped.
B, I am a returning “customer” and have had no problems with the other pamphlet’s.
This leads me to ask why you don’t ship to the UK? I love the books and wouldn’t mind helping to support future research by buying an item or two.
Sorry for whinging on, but I think what you have done with this research is important to us all.
Thanks again, Mark.
I believe this has been fixed. Out of US orders should still allow downloacs.
I just paid for the download and got an error as well. Also there is nothing to use on your “Contact” page.
Is the pamphlet available as a pdf? I just tried to purchase it and it says you do not ship to Australia. Thanks.
Sorry, just read the comment above and now realise that it is a pdf download. Perhaps you could provide another link for the download that doesn’t require going through your cart/checkout process so that international readers can have access to it?
I’ll see if we can do that.
No problem downloading. The exercise is a wonderful mind opener. I wonder if all geometric shapes can be produced using only a straightedge and compass? Thanks.
All the regular polygons can be constructed with these two simple tools. Most don’t need you to make adjustments (“neusis” constructions) to the compass to fine tune the construction–what they used to call “rusty compass” (i.e. stuck in one place) constructions.
This is quite false.
The answer is no. A regular n-gon is constructible with straightedge and compass if and only if n = 2kp1p2…pt where k and t are non-negative integers, and the pi’s (when t > 0) are distinct Fermat primes. (A Fermat prime is a prime number of the form {\displaystyle 2^{(2^{m})}+1.} {\displaystyle 2^{(2^{m})}+1.})
Thanks for the correction Donald
I see that did not format well. I try again.
A regular n-gon is constructible with straightedge and compass if and only if
n = 2^k p_1 p_2 … p_t ,
where k and t are non-negative integers, and the p_1, …, p_t are each distinct Fermat primes (when t > 0) .
(A Fermat prime is a prime number of the form 1+2^(2^m) ).
So for n <= 16 , if n = 3, 4, 5, 6, 8, 10, 12, 15, 16, then an n-gon is constructible
but if n=7,9,13, or 14 , then an n-gon is not constructible.
See https://en.wikipedia.org/wiki/Constructible_polygon for more details.
Although it is possible to construct a regular pentagon using a straightedge and compass, I give for example such a construction in http://www.math.mtu.edu/~kreher/ABOUTME/pentagram.pdf,
apparently Durer’s construction construction does not yield a regular pentagon, the lower right angle of the red pentagon shown above is ≈ 108°21’58.03259 and not exactly 108° as required.
See: https://arxiv.org/pdf/1205.0080.pdf for an excellent discussion on “The Polygons of Albrecht Dürer”. Many of the the approximate constructions provided by Dürer were typically those used in the workshops of engravers, cabinetmakers or masons.
Thanks again Donald. These were very useful and appropriate..I’ve printed them out for further study.
You are welcome.