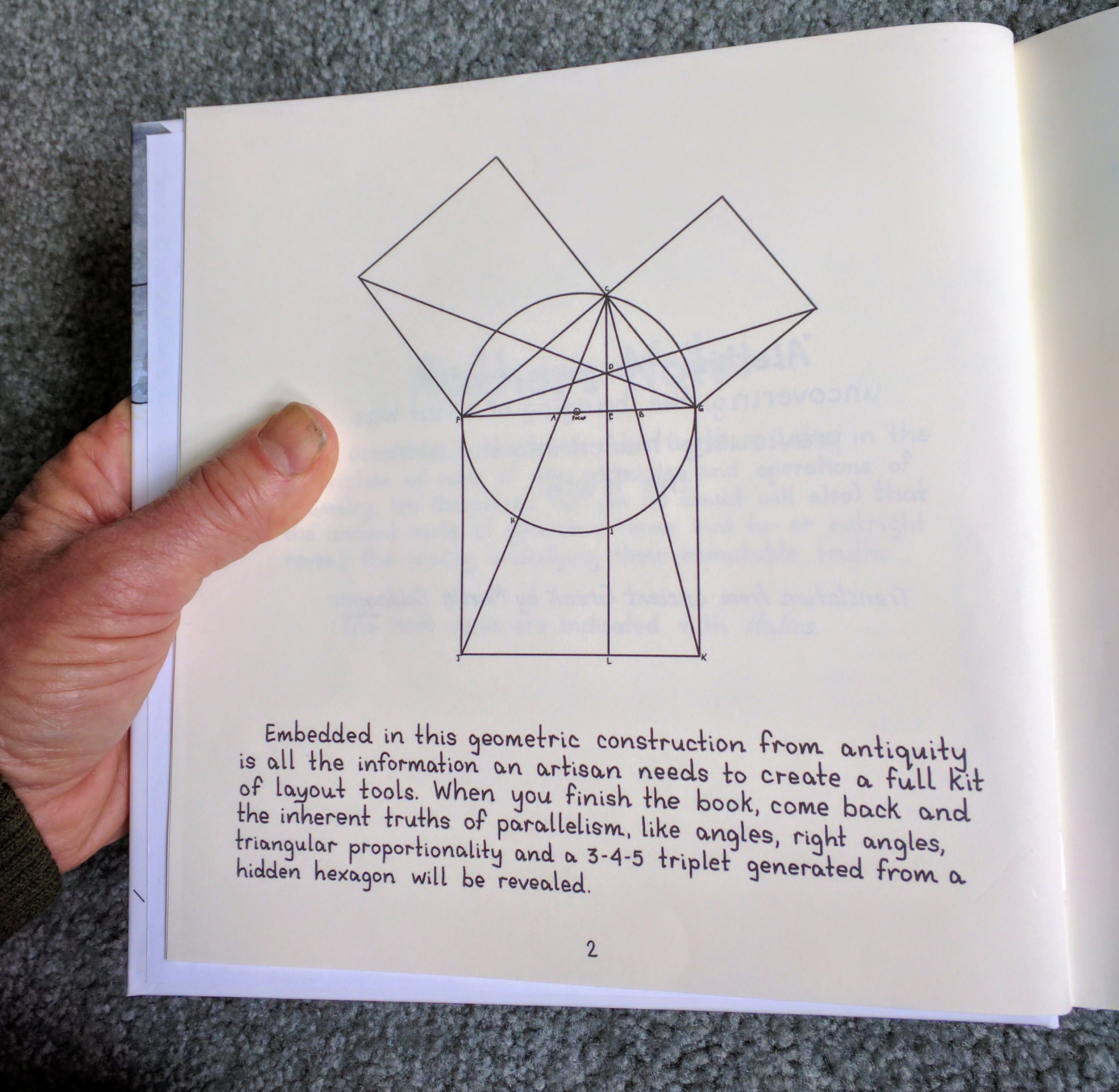
You may remember this page from the introduction to “From Truths to Tools“:
We’ve had a few folks ask about the “hidden hexagon” mentioned in the text, and we think it’s time to share the answer with everyone. This also means revealing a little bit more about what is going on (and not going on) in this geometric construction.
What is going on is this: Drawing lines from and through certain points seems to magically create a representation of one of the most important, not to mention useful, theorems for artisans in geometry: the Pythagorean Triplet. In the geometry of this particular interaction of a circle with a square, a triangle is formed in the upper half of the circle whose legs go on to generate a pair of squares that, when their areas are added together, equal the area of the lower square — and they do that in what looks to be a simple triplet ratio of leg lengths of three to four to five.
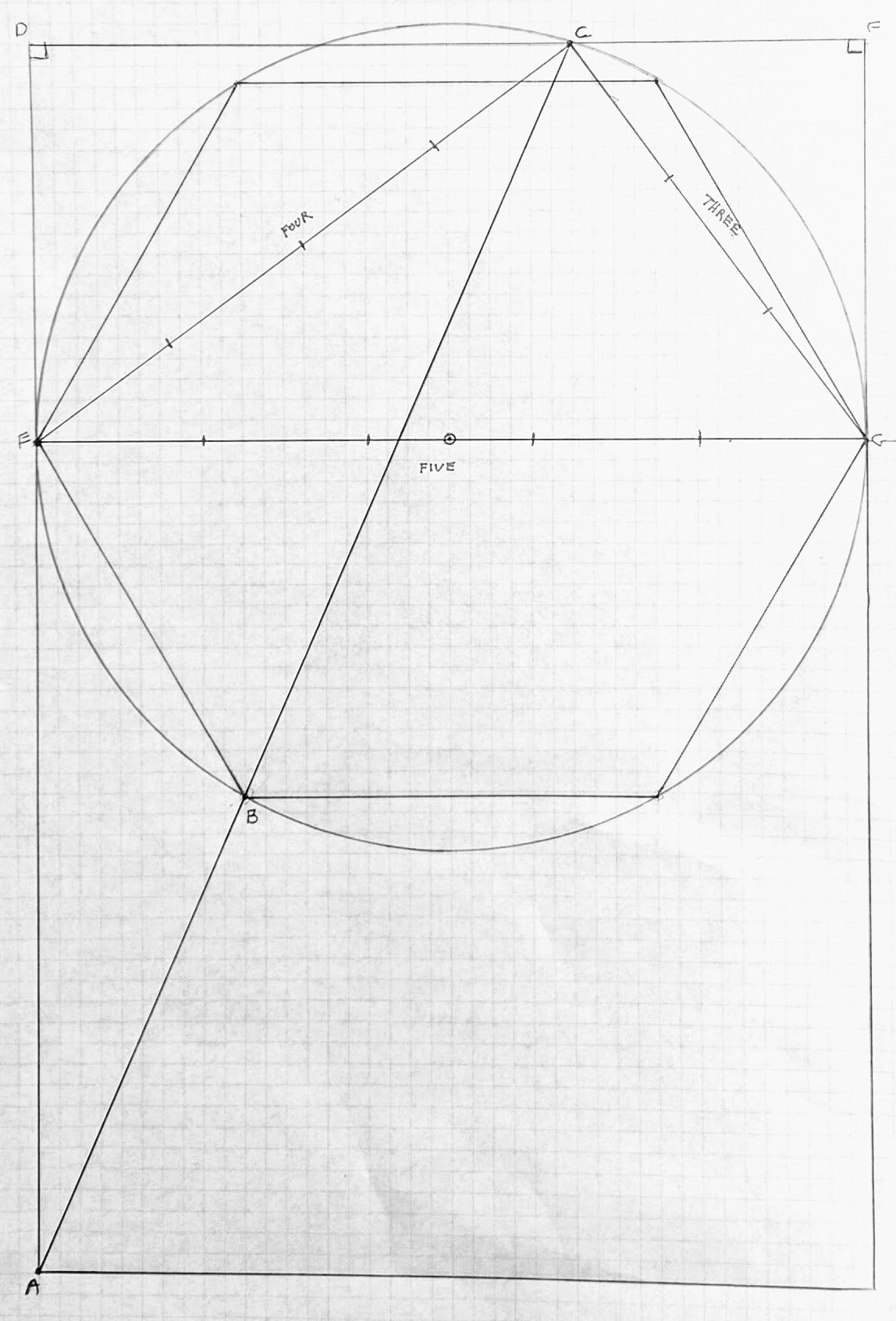
To arrive at the correct root lengths of the upper two squares to make this simple ratio happen, the trick from antiquity is to generate a hexagon inside the circle (by stepping the radius of the circle around its circumference) and to then draw a line from the lower left hand corner of the lower square through the vertex of the closest hexagon facet. Next, you continue the line to intersect the upper portion of the circle. This provides the point to which you then draw the legs of the triangle.
The results are leg length relationships of three segments to four segments to the five segments of the diameter line. We have just revealed the simplest of the countless Pythagorean triplets. But have we really? The answer is: Almost, but not really.
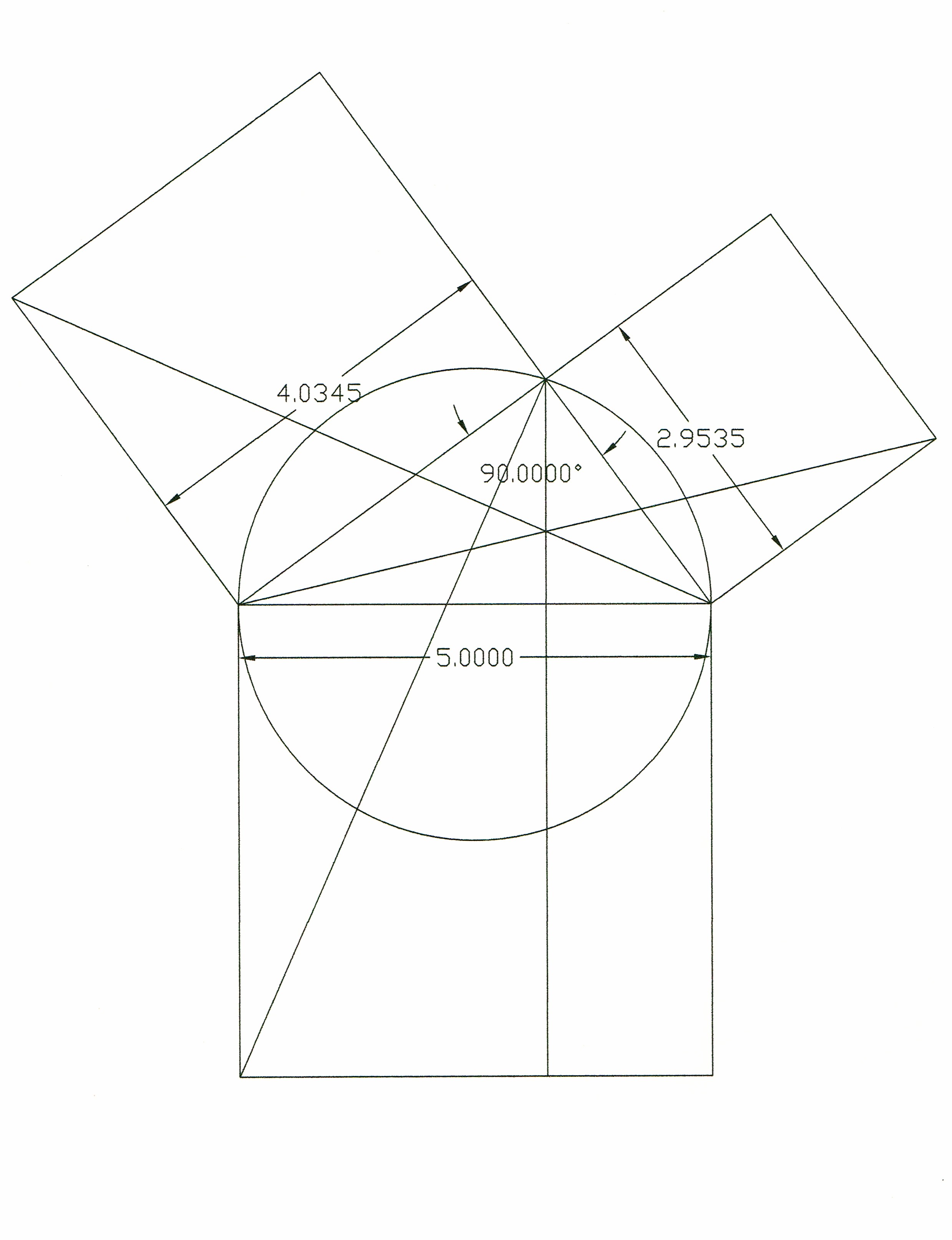
We had our friend Dr. Francis Natali take a look at it, and after a couple pages worth of quadratic equations, the truth was outed: The whole-number relationship just isn’t there – though it is, inexplicably, amazingly close. Another friend, Kit Africa, generated the drawing above via CAD, also revealing an oh-so-close 3-4-5 triplet. The bottom line: This drawing from antiquity is apparently symbolic: It celebrates the interaction of easily generated shapes that allowed artisans to intuitively design and build beautifully proportioned and aligned forms on the principles of simple plane geometry.
— Jim Tolpin, By Hand & Eye


Very interesting!
One thing keeps me wondering…if I draw (also via CAD) a line which is 5 and then two circles from the endpoints (3 and 4 as whole-number), then connect the endpoints from line 1 with one intersection of the two circles, the included angle between those 2 lines is 90 degree even.
So the Pythagorean theorem seems to be correct. 😉
Why is the angle in your example also 90 degree even? Any thoughts?
Your 90 degree angle will always be perfect, even if you move the point all around the hemisphere of the circle, your A and B sides of your circle will change in length, from an even 3 and 4. In the formula (A sq + B sq = C sq) your C will always be 5 but your change in A & B will still work on the formula, just not in whole numbers.
In the example given: C is not 5 its 5.00003525.
I’m guessing that C is 5 and was the only constant set in these calculations. Note that every number displayed is given to four decimal places, so 4.0345 2.9535 are probably rounded approximations based on the output settings of the CAD software.
But Jim Tolpin writes : “Dr. Francis Natali take a look at it, and after a couple pages worth of quadratic equations, the truth was outed: The whole-number relationship just isn’t there – though it is, inexplicably, amazingly close.” Hence I don’t think these are output settings of the CAD software. To be sure I will have to check the math myself, but not today. I have other pressing math issues to settle.
Correct: Five was the set (given) line segment length.
Thanks mcdara,
Now I got it – Thales theorem.
I should have answered that myself.
I don’t believe the slight error is in your 3-4-5 ratio or in your squares shown above, but in your A-B-C line generated referencing your hex within the circle. Your point A actually will hit a point .0914 below the “5” square corner
Close enough for pyramid work.
Jim, now that I look again I realize that what your saying is right, if your line is from the “5” square lower left corner, the point you hit on the circle will be slightly off of the 3,4,5 triangle and so the ancient diagram is not quite perfect.
I think that within the limitations of hand tools, it is “perfect” enough. Even using a modern ruler and dividers there is room for error in the width of the markings. The error is not enough to disturb the proportional relationships which is why the Masons decided to use it for its symbolism.
I find it hard to belive that this was the method from antiquity used to draw the figure you show on page 2, because there is a simpler straight forward straight edge and compass method to accurately the correct figure. What is your source?
Could you illustrate the example of which you speak please while someone looks for “your source” for you?
I very much enjoy this subject mater as a Timberwright, and have found similar anomaly as Jim T. has shared in this post…
Donald: I also doubt that they used this construction for any practical purpose. I learned of it by studying some of the geometric esoteria associated with the ancient order of masons.
Thanks. Very reassuring. Maybe I will buy your book.
I’m still trying to figure out how the ancient greeks constructed the star of pythagoras. I can do it after a little algebra that I don’t think they knew. It was required to enter the society (or cult) of pythagoras.
Thanks again for this post Jim…
I can’t speak to “practical” or even common but this was (and is employed) both historically and today…or at least the understanding and knowledge of this and various other geometric esoteria, such as pentagram and related are discussed and employed in both our masonry and timber framing…I agree rare but not forgotten or unused…
Me and my big mouth.
O.K. here we go.
1.Mark points A and F and draw line AF.
2.Divide L into 5 equal segments ( see https://www.mathopenref.com/printdividesegment.html )
marking points B,C,D,E, between A and F, so that |AB|=|BC|=|CD|=|DE|=|EF|.
3.Set compass on FC and draw circle S of radius FC centered at C. (You only need a small arc above line L.)
4.Set compass on AE and mark S at the intersection of the circle of radius AE centered at A .
Call this mark the point G.
5. Draw AG and FG. (So AFG is a 3 4 5 tringle.)
6. Construct squares with sides AG, FG and AF
(see https://www.mathopenref.com/printsquare.html )
Now you are basically done. However to continue:
7.Construct perpendicular bisector of AG at Y.
8.Set compass on YG and draw circle of radius YG with center Y.
9.Drop line perpendicular to AF from point G until it hits the bottom of square of side AF.
10. Draw rays from the points A,G,F. to the corner of the squares opposite these points.
So the Hexagon seems to me to be immaterial. And if you do inscribe it in the circle I think it will
likely not have a corner at the intersection of the ray from G and the circle with radius YG, but you won’t be able to see it, because your pencil is too fat.
(I hope this is correct. I am not a good proofreader.)
The hexagon is not immaterial in that it is a curiosity that hopefully opens your “minds eye” to seeing other relationships within the figure. It is a delightful mind exercise.
Can you give some explanation? How does it help see other relationships within the figure?
Don, the book is an excellent source to explore the use of dividers and rules. As you construct the drawings shown by Jim, use your dividers and rule to add additional lines that either extend through different points or with the same spacing’s. As you add geometric shapes, see how they look in proportion to one another. As you do this, consider that the dimensions aren’t as important as the proportions. You just have to do the drawings and play with them until you have that “ah ha” moment.
The irony here is that the lesson of the article is that trusting your “inner eye” and abandoning logic gives misleading results. The “ancients” required proof before accepting the results of a construction.
It’s easy enough to demonstrate that the construction using the vertex of the hexagon doesn’t result in a 3,4,5 triangle. No quadratic equation are necessary, only basic logic.
I can barely read it, but I’m seeing the lower left corner as J
We are given that FG is 5 units long. FJ is then also 5 units long.
Drop a vertical line from H to line JK. Label the intersection M.
JM is 1/4 of 5 or 5/4 units long.
(FHCenter is an equilateral triangle so a vertical line through H bisects FCenter)
The distance from point H to line FG is 5/4(sqrt3)
(sides of 30,60,90 triangle are x,x(sqrt3),2x. in this case x= 5/4)
MH is 5 – (5/4(sqrt3)) units long.
All we have to do is assume that we have a perfect 3,4,5 triangle and see if the ratio HM/JM of the construction given = the ratio CL/JL of the correct construction
Since FG = 5 units, using similar triangles we see that CE = 4/5 x 3 = 12/5 units and that FE = 4/5 x 4 = 16/5 units long
Sticking with whole number ratios CL = 25/5 + 12/5 = 37/5 units long
CL/JL (correct construction) = (37/5) / (16/5) = 37/16
HM/JM (given construction) = (5- (5/4sqrt3)) / (5/4) = 4 – sqrt3
Does 4 – sqrt3 = 37/16 ???
If so, -sqrt3 = -27/16
Square both sides
3 is not equal to 729/256 so the construction given is incorrect
Jenohdit: This was the same line of reasoning my friend Nat pursued with the same conclusion. I wonder, since the error is within a pencil width as also pointed out here in the comments, if the artisans creating this construction realized the inherent error? I’m betting they knew it wasn’t strictly true, but, like so many other geometric tricks of the trade, it was good enough for practical applications.
I’m wondering if anyone else has done this with a really good divider?
I have tried and it seems visible to me?
Anybody else?
“…We are given that FG is 5 units long. FJ is then also 5 units long…”
???…Doesn’t seem to be in my model…Not by a long shot…
Did I miss something?
Silly me…wrong model…
I have checked your math and it is correct.
I meant I have checked over what jenohdit wrote and it is correct.
Line 3 is wrong. You have to center FC at F not C. But having said that, I agree with the idea that the Hex is immaterial. I see that the idea of the Hex is to connect the vertex of G to the lower left corner of your “L” square. That’s when the error appears (assuming, as you did, that you start with a perfect 3-4-5 triangle). it misses it by 1/32, which is a visible error. If you had a reason for this exercise, you could rotate your Hex .0157 (slightly over 1/64) clockwise, and you would connect your line from the vertex G through a vertex on the hex to the corner of your square.
I will say, I much prefer the exercise Jim and George showed me at Amana, on how to use this to make a accurate “template” to build my wooden layout squares.
Probably so. It is a pity I cannot correct it.
I suspect but it is not completely clear, that this “hexagon” derives from Albrecht Dürer book “Underweysung der Messung mit dem Zirckel und Richtscheyt”, where it is reported that he includes many approximations to geometric figures without saying so. Hence misleading readers and corrupting generations. Approximation is fine for art work, but not for precise woodworking or machining. Hence I maintain that the addition of this “hidden hexagon” is not only inmaterial it is also perhaps harmful. But I have ordered Jim Tolpin’s book to see what it says and I do not pass judgement here. I am sure it is fine. I am also sure if the reader is told it is a “Hidden approximate hexagon” (with appropriate explanation) there would be no controversy. There is however as we have discovered in this discourse no hidden true hexagon here.
Thank you buh what is it all about…explain plese
Sent from Mail for Windows 10
I think to understand that we need to buy the book. The caption to the figure on page 2 indicates that this figure is all that is needed to create a full kit of layout tools. So I guess that is what it is all about.
From my perspective and application…It does first what Eric above said…it opens the mind’s eye…
From there, you can see proportions and design with them in a more empirical fashion (or at least I can..)
Set dividers, make story poles, layout around curves of logs, create geometry for joinery…and the list just rambles on…
Well I ordered the book, just to see what it says. I hope it will ship soon as I am moving.
I barely passed algebra in school, but excelled in geometry. After attending reading “By Hand and Eye” and attending a class with George Walker, I realized the short comings of my extensive education. Why am I now just finding out these truths?
Another book that closely relates is “Flatland”. It can be read in one sitting.
As a former “educator” within the system..it is easy to see why our educational system is broke…This very conversation illustrates it brilliantly…
True “fundamental application” of tangible skill sets are no longer taught…or thought of as having any value…How many here understand “from scratch” basics of gardening, cooking, tailoring, or just general foundational life skills…let alone doing those basic things for themselves..???
Thanks for the book lead to “Flatland,” a good read all here would probably enjoy.
I’m curious to know what truths you have recently been made aware of that you didn’t get when you were excelling in geometry in school.
A sixty fourth for the 3 side and half of that for the 4 side.
On a framing crew calling out sixteenth might find a thrown hammer coming your way.
Hmmm…LOL…it does depend on the crew I suppose…???
4.0345″ would be way more than a 1/64″ to the “fat” I think? (aka: more than 1/32″ actually)
If I made a tenon that “fat” that had to go into a mortise that much undersized…someone on our crew would throw more than a hammer at me on raising day…LOL!
We timber frame in metric and we build to 0.5mm in layout…
Old adage…”Aim small, miss small.”
It’s all a perspectives on the systems we employ I guess, or the tolerances we follow?