
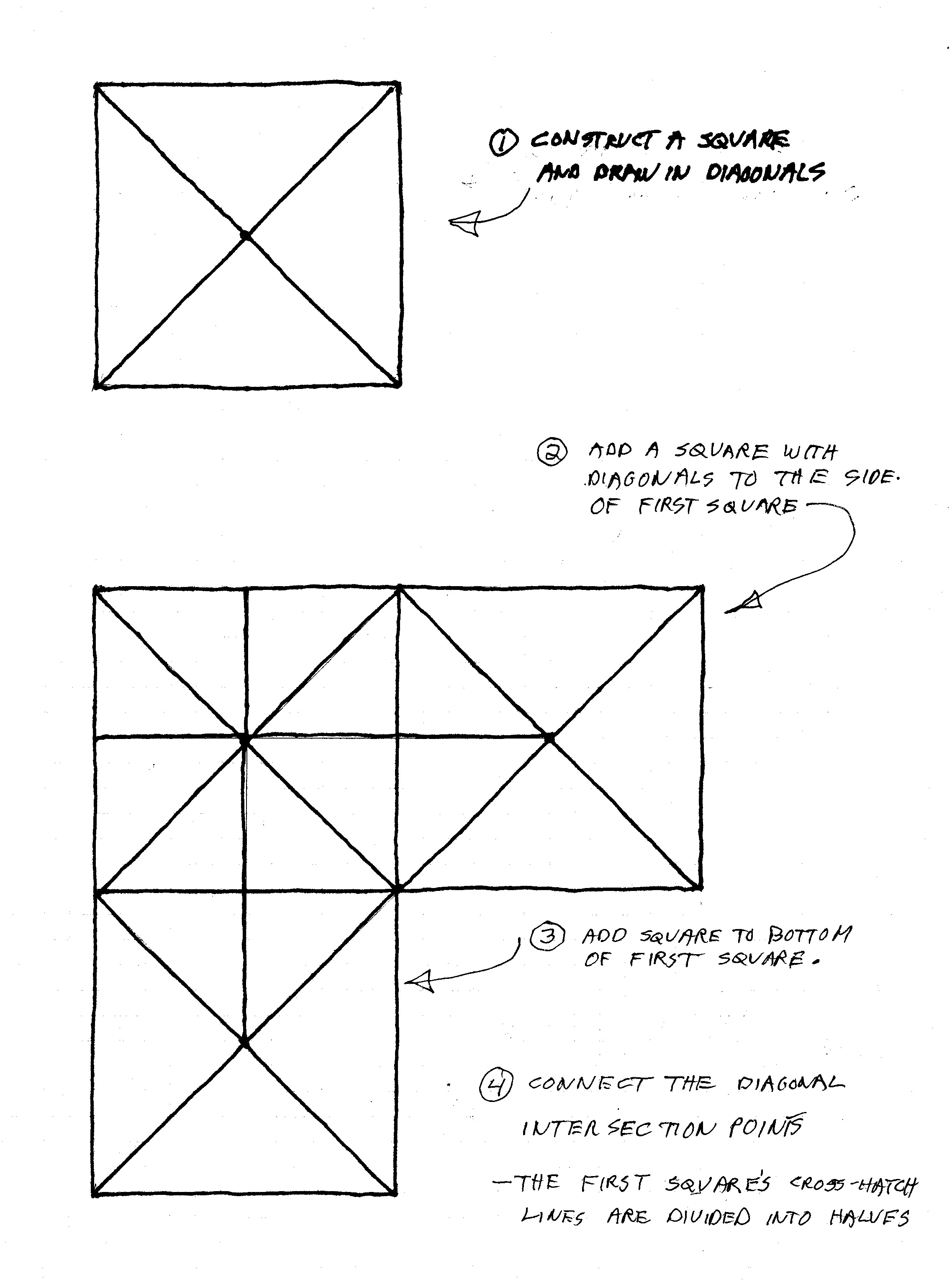
Yes it’s fine to think inside the box for a change, especially when there’s no need to think at all! At least not if your goal is to divide the box into any number of divisions. Thanks to the geometry of diagonal lines that occur inherently within a square, you need only a straightedge to reveal these fractions. This truth/tool allows you to lay out the baffles that will keep the bottles of spirits from rattling or worse. Of course there are easier ways to come up with these fractions (the sector springs to mind), but this is still a great way to construct by hand and observe by eye these geometric patterns as they spring to life.
See if you can follow the steps below which I’ve sketched on a sheet of graph paper. Why don’t you grab some paper and follow along too? Bet your kid can (and would like to) help you out! Get out a pair of dividers so you can confirm that the intersections do indeed produce perfectly spaced segments along a line.
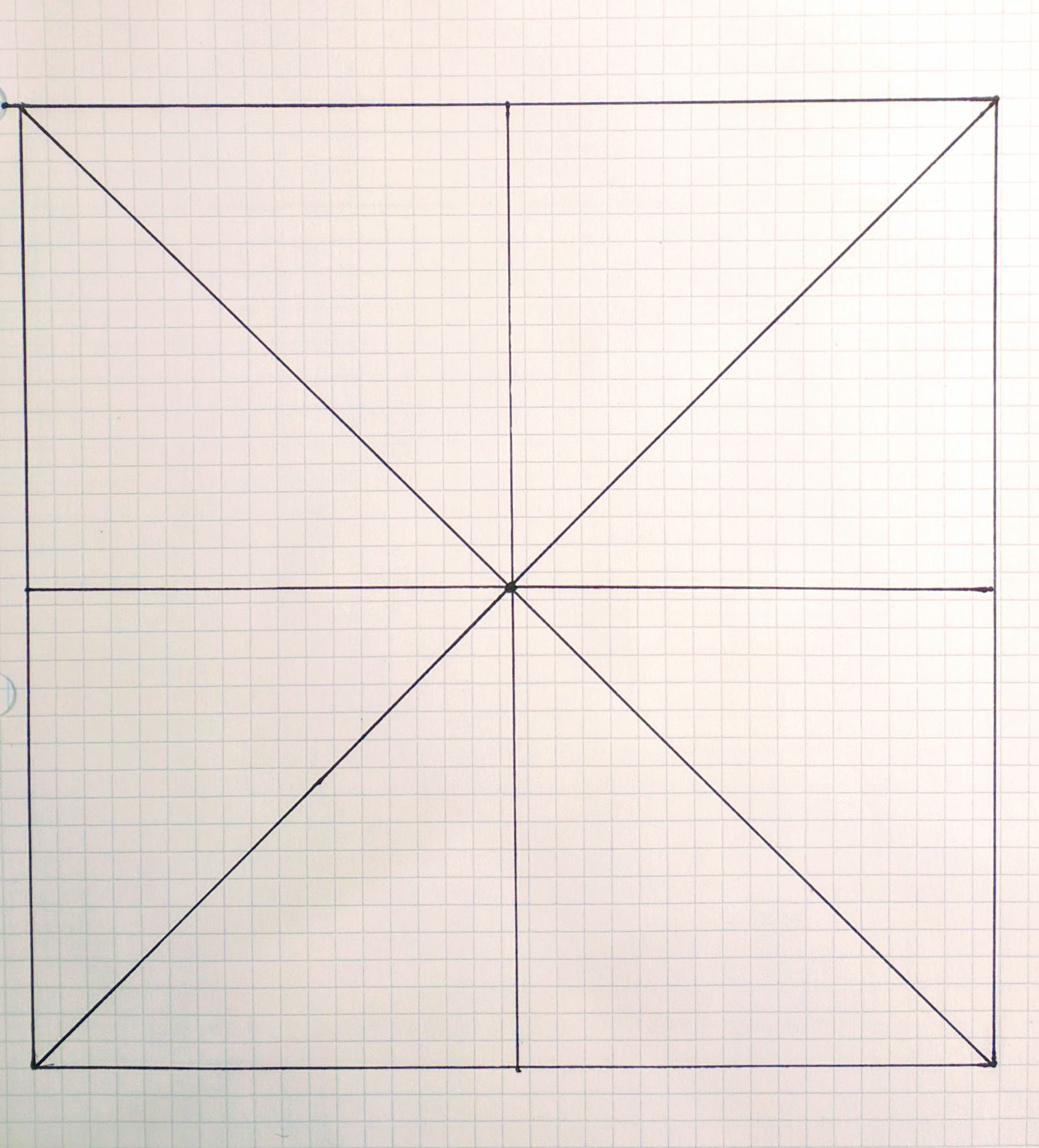
Now isolate the first square…
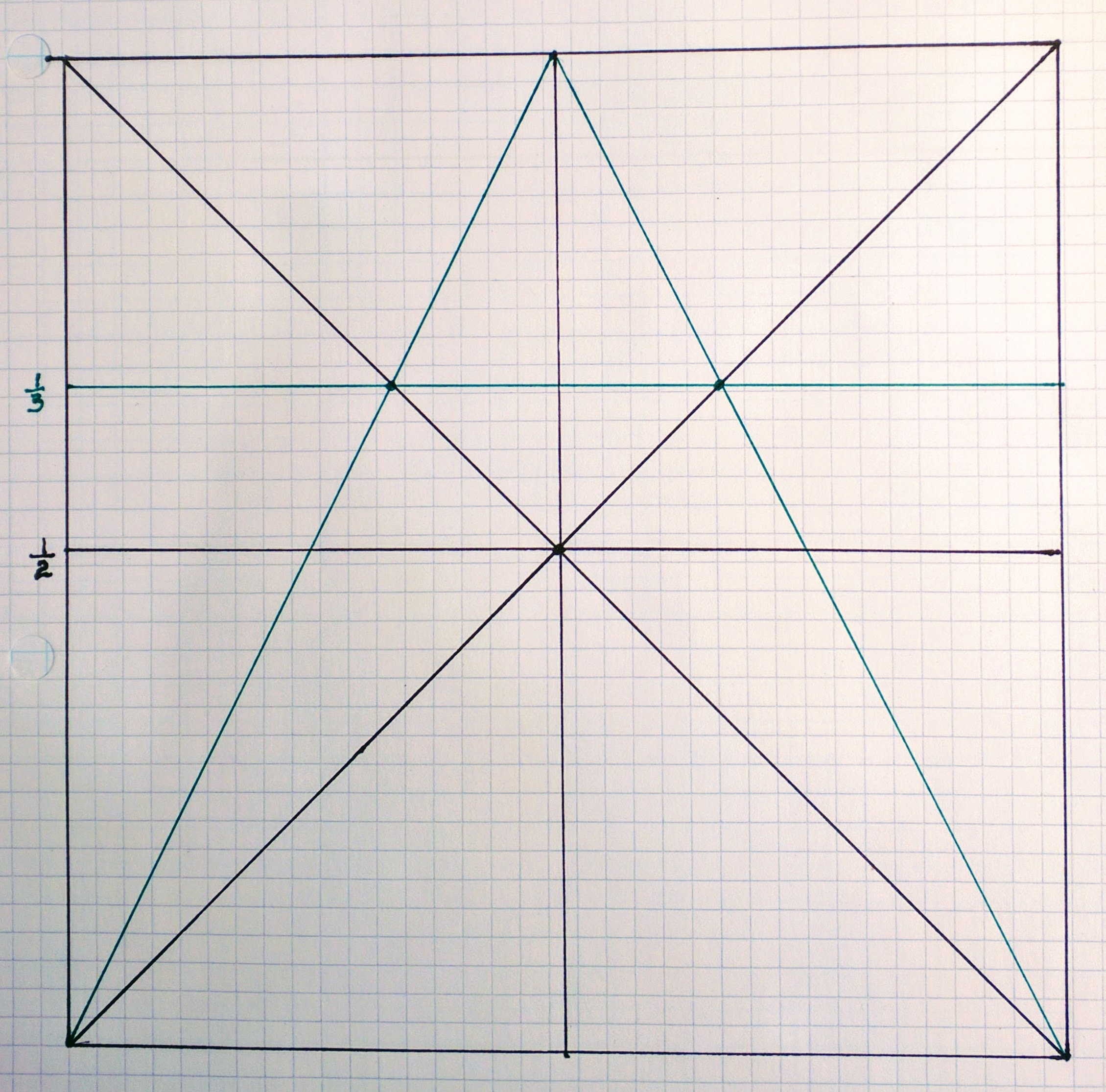
…and continue by drawing a pair of diagonal lines as shown in green in the next sketch:
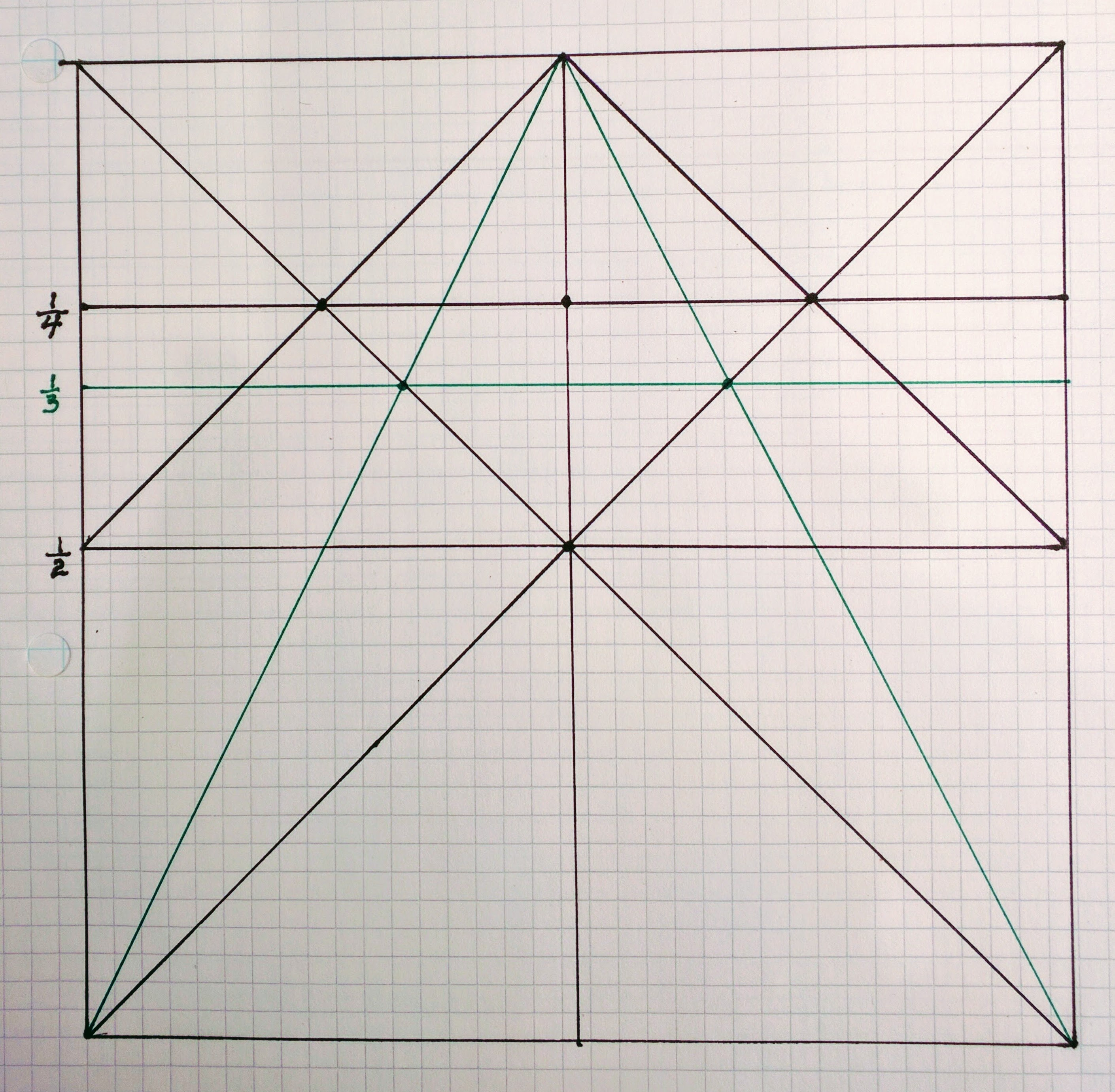
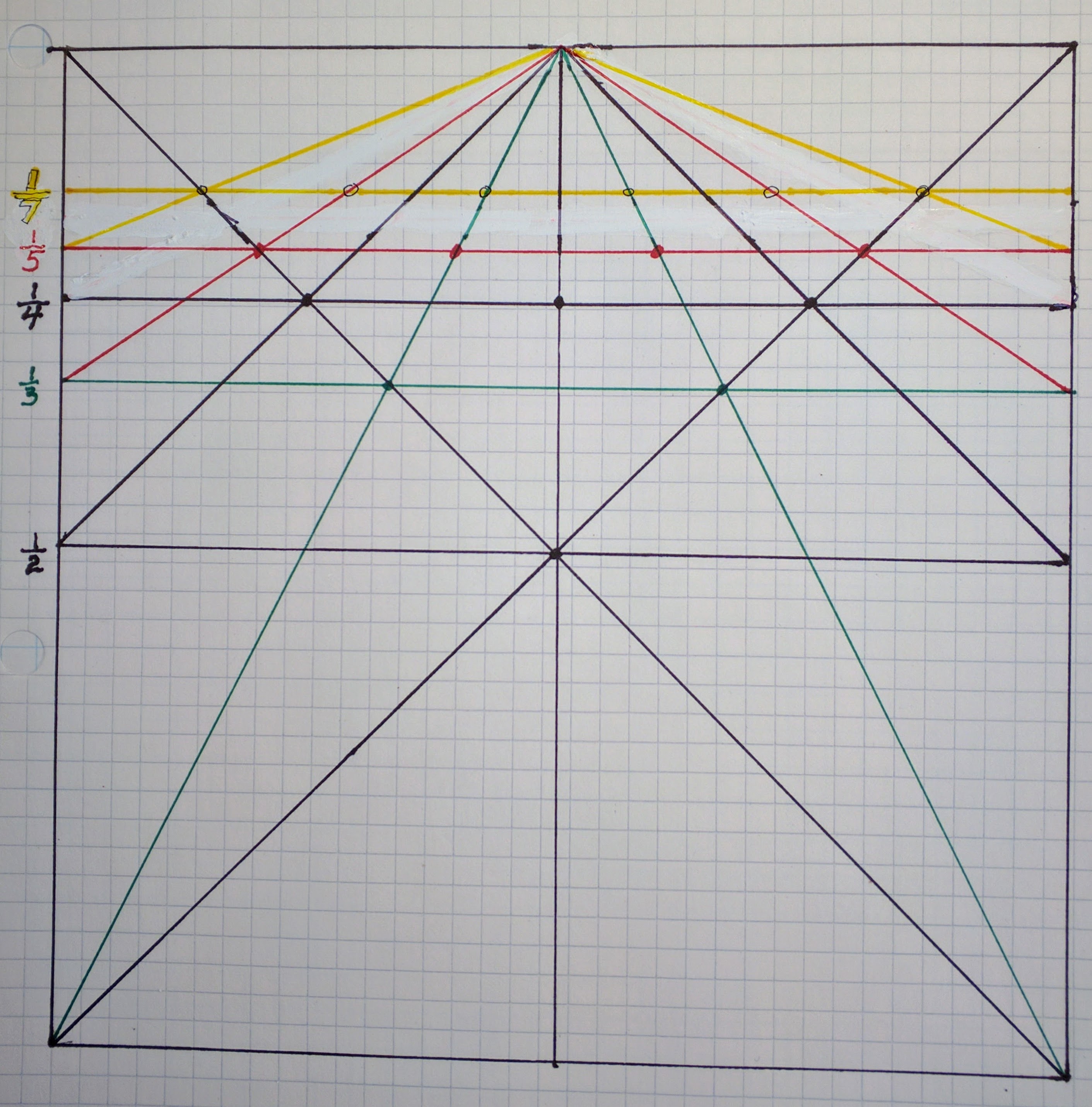
Next draw a horizontal line through the points that have been given to you where the (green) diagonals cross the first set. If you set your dividers to the intersections along this new horizontal line, you’ll find there are exactly/precisely/perfectly three equal-length segments. Now let’s draw another set of diagonals and connect their intersections with the original diagonals with a horizontal line:
As your dividers will reveal to you, that line is now automagically broken into four equal segments. Let’s continue the process with two more sets of lines (I really do highly recommend that you stop right now and grab a sheet of graph paper and watch this happen in real time through your own hands and eyes).
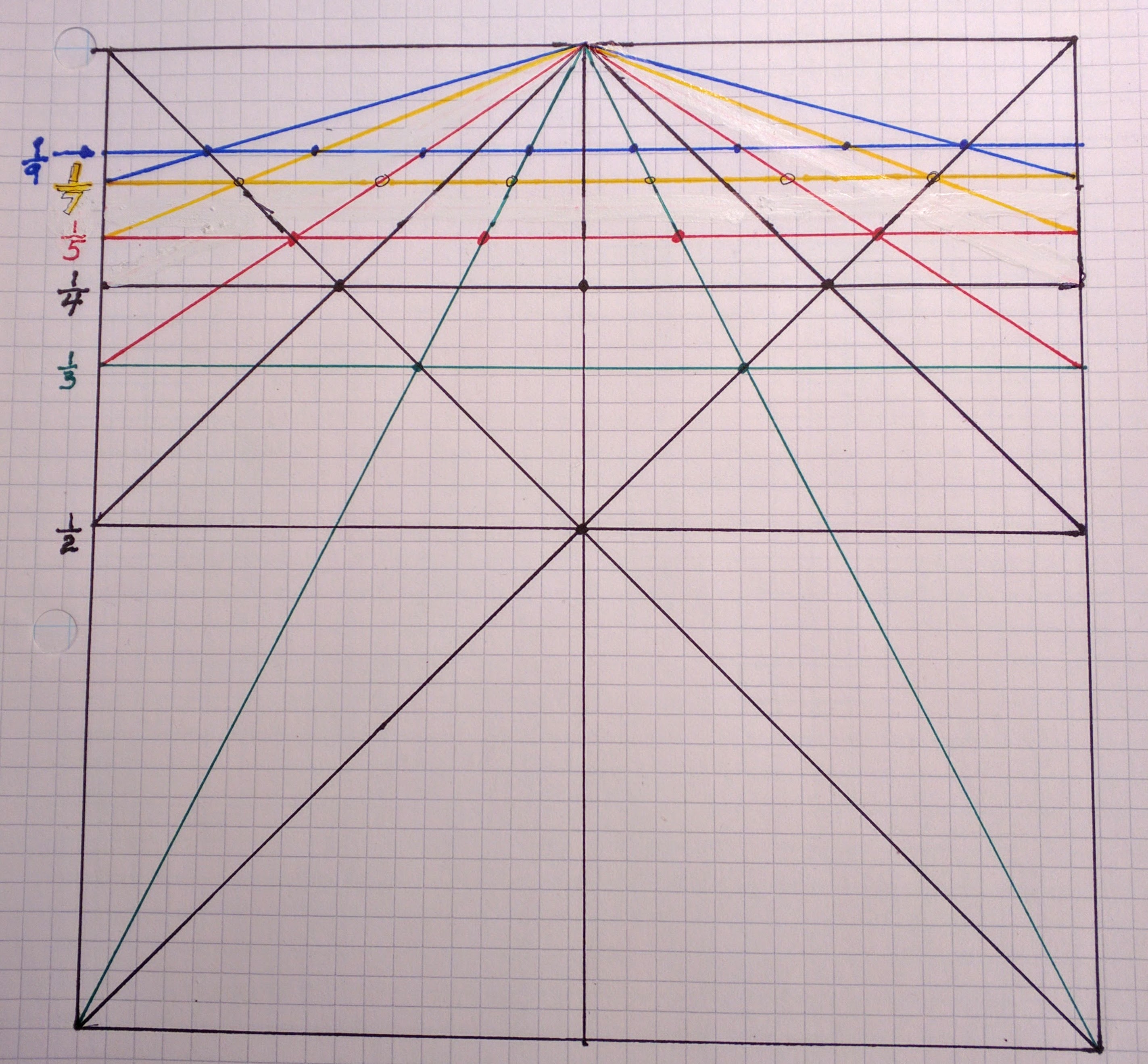
You’ll discover the red lines produces fifth segments while the yellow produce sevenths along their horizontals. Add another set (in blue here) of diagonals and horizontal and you come up with ninths:
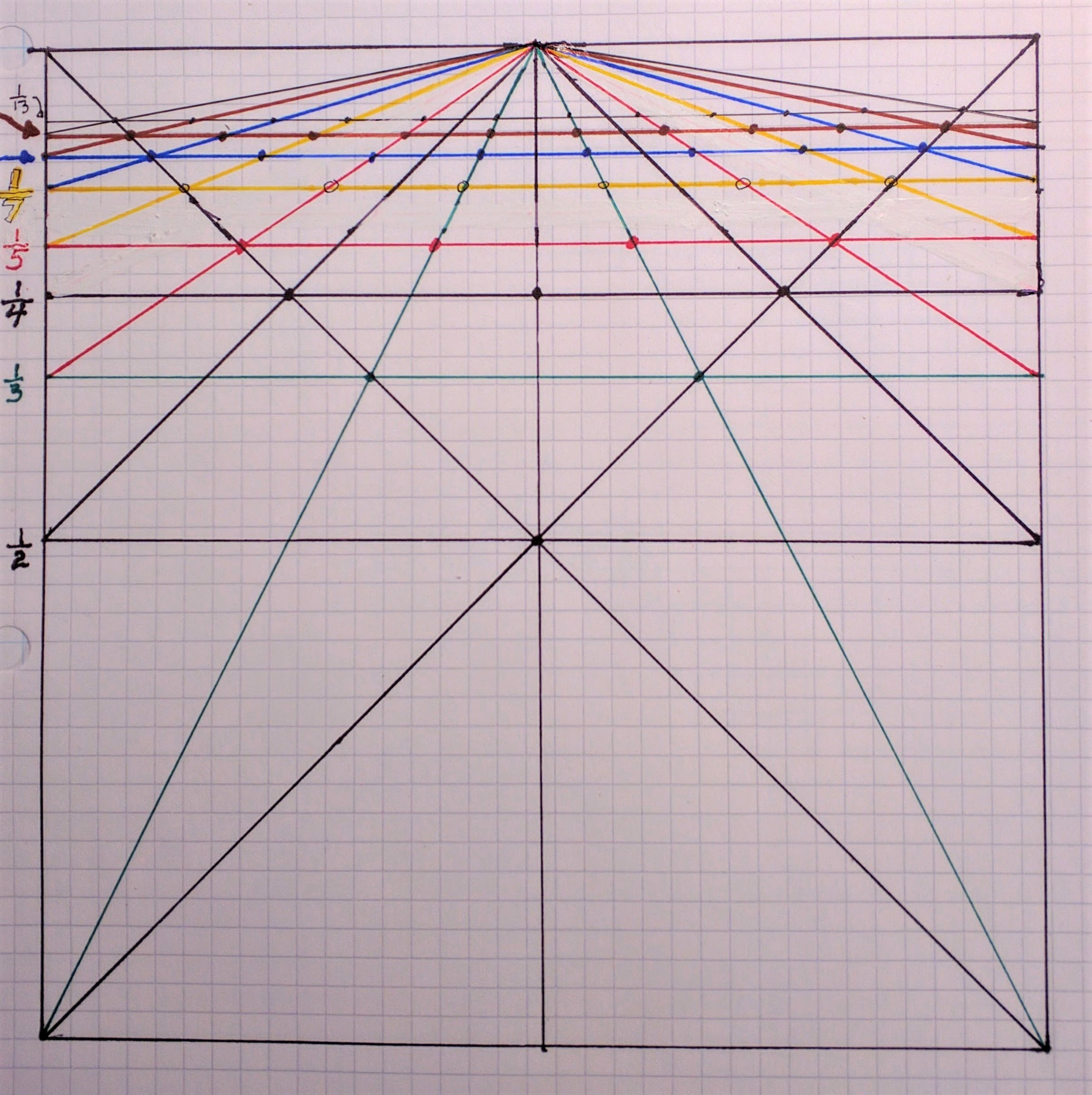
Keep going if you like:
You’ll get ninths, elevenths and thirteenths – and on to infinity I suppose. What if you want an even number of divisions along a horizontal line, say tenths along the line of fifths? Well they are there waiting for you to discover with your dividers!
— Jim Tolpin, one of the co-authors of “From Truths to Tools“

I noticed you white-outed the diagonal to the 1/4 endpoint. Would this have created the 1/6 diagonal? You appear to be showing only the odd-numbered ones. (Too many lines? Try drawing a seven dimensional cube.)
Not sure if it properly correlates, but you bring out 1/3’s, 1/4’s, 1/5’s, 1/7’s, 1/9’s, 1/11’s and 1/13’s. Those also happen to be specific musical intervals in western music. Wondering if Pythagoras might have something to say on this.
I wonder what Hippasus might have to say.