Once upon a time, 10′ poles were a tool common to a number of trades including linemen and cemetery workers. What they touched with their 10′ poles – high-voltage power lines and corpses respectively – is not something most people would want to touch, not even with an 11′ pole.
Carpenters, however, were quite happy with the 10′, or as the drawing suggests, any length of stick divided into 10 equal segments. For in their hands lay a tool critical to the efficiency and accuracy of their layout work. As we discuss in our book “From Truths to Tools” a right angle can be formed by a triangle composed of three whole-number leg lengths. In the simplest triplet, the leg lengths are three, four and five “whatevers.” The 10′ pole simply employs a doubling of those numbers: six, eight and 10, which are measured in this case with the imperial feet of some long-dead king. (If you think feet stink, you could measure out the pole in the cubits {forearm lengths} of some even longer-dead pharaoh.)
As demonstrated below – lifted from the book – we can construct a “proof” of this particular triplet using a straightedge and dividers. Be aware that there are many more whole-number triplet combinations – perhaps an infinite amount.
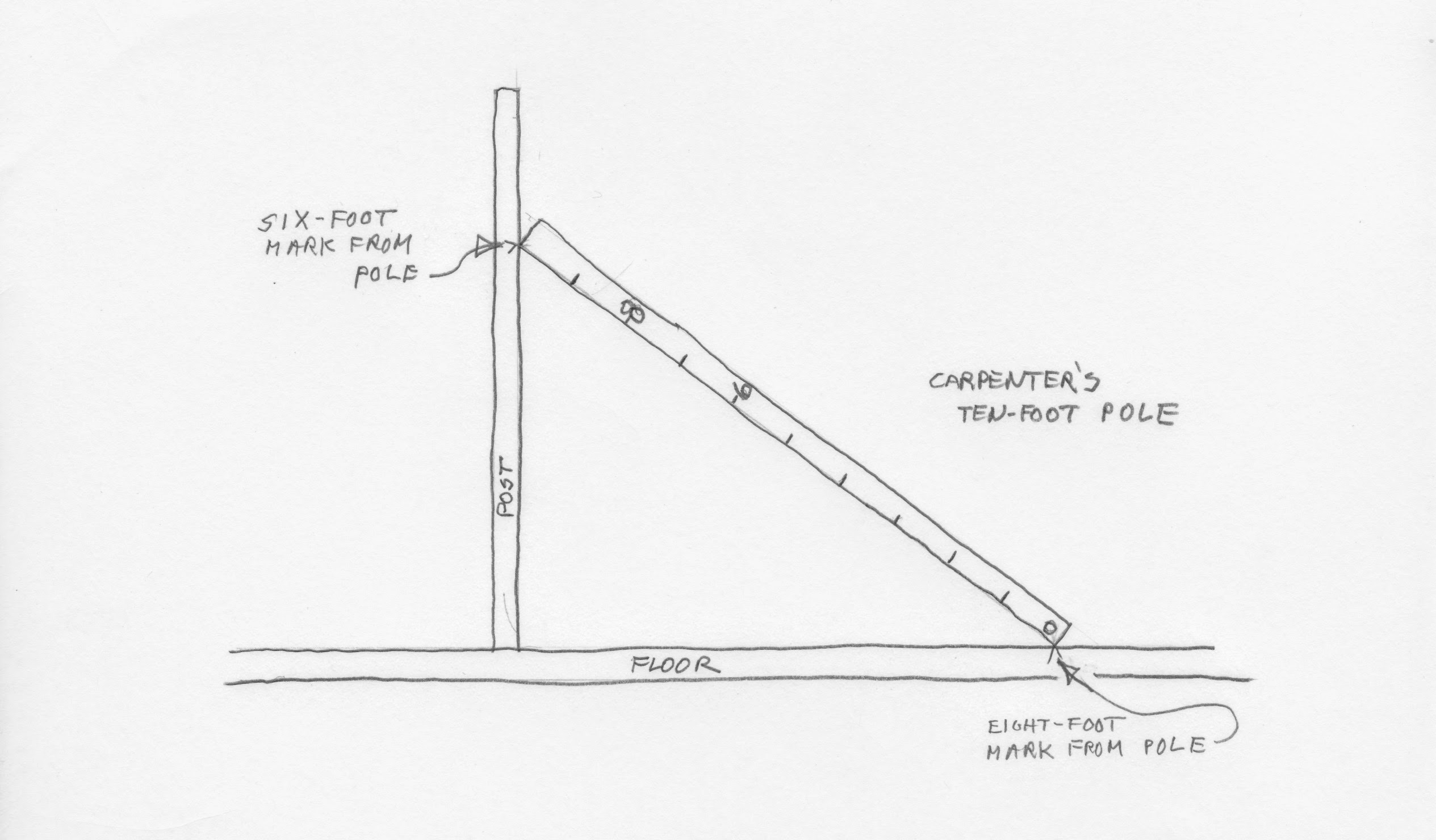
The sketch below shows the pole in use aligning a post square (and therefore plumb) to a level floor:
It’s a simple enough procedure: After fixing the base of the post to the desired location on the floor system, you use the pole to lay out a mark 6′ up from the bottom of the post. Next, you lay out a mark 8′ away from the post on the floor. When the full 10′ length of the pole fits exactly between the mark on the floor and on the post face, your post will be exactly square to the floor. Turns out that this layout problem (among many others as you’ll discover in the book) can be beat with a stick!
— Jim Tolpin, byhandandeye.com

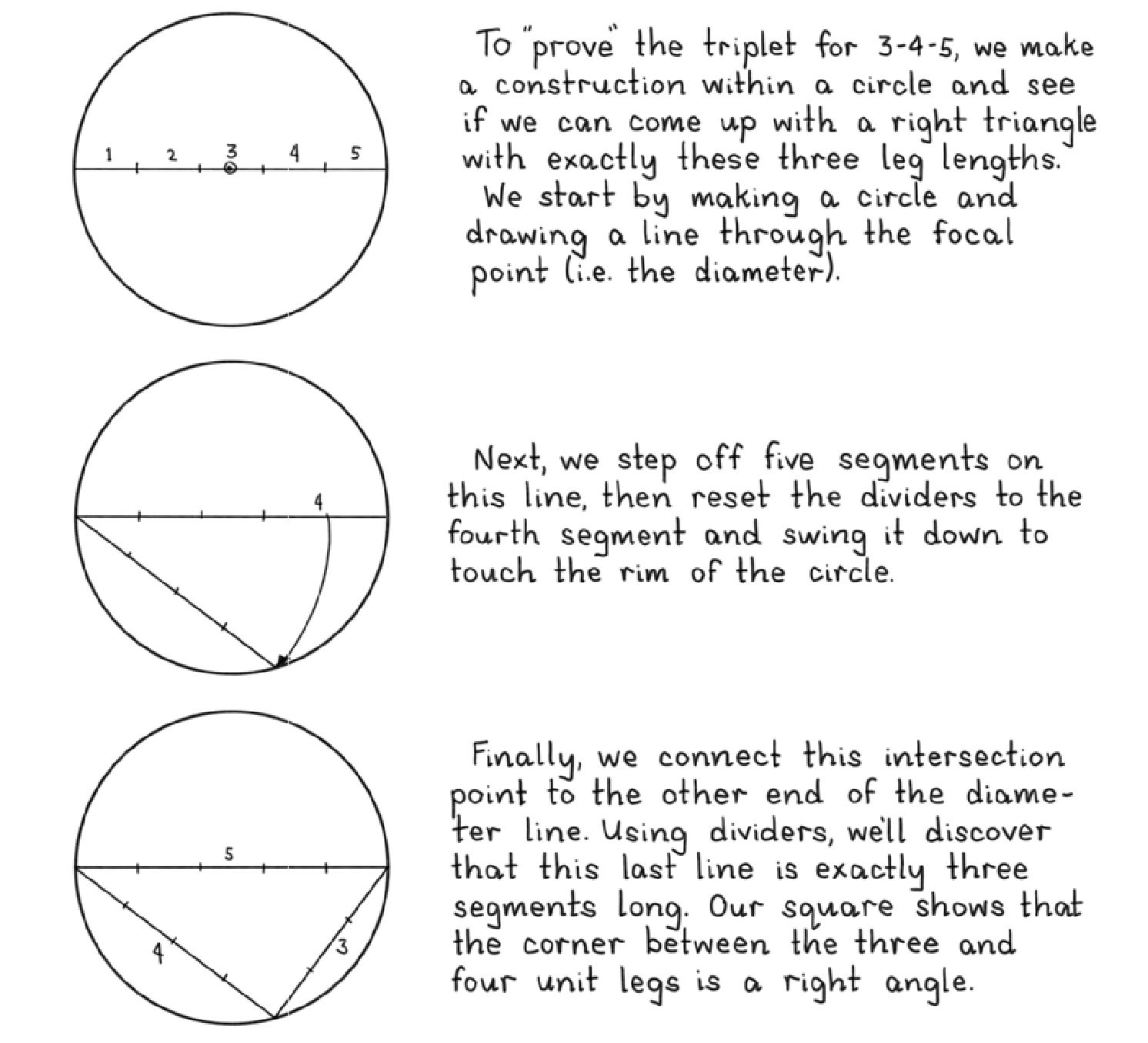
3-4-5 Rule or pythagorus in application.
Carpenters also often used the 5-12-13 triplet rule to generate the ubiquitous 5-12 pitch roof systems.
Now THIS was an interesting bit of history. I’ve head the expression all my life, but never knew the origin.
There is obviously a need among woodworkers for a practical (and readable which these books do well) treatise on shop geometry, but that’s a curious use of the word proof in a geometrical context. Theoretical rigor may be boring, but anyone who needs this training probably needs it due to having avoided rigor in high school geometry. Teach a man to fish…
The circle is entirely unnecessary since it has nothing to do with the conclusion or the construction even.
The line was divided into 5 units which has nothing to do with the circumscribed circle. A circle of 4 units on on end and one of 3 units on the other would intersect at that same point. There is no need to divide the 3rd side since it’s length was given in the question as were the other 2.
The larger circle might have had some use if the point was to actually prove that the resulting angle was right instead of measuring it with a square. Classical geometry is compass and straightedge only, no angle or length measurement. Practically speaking, dividing lines and measuring square has great value, not true for theory.
It is true that a triangle whose base is the diameter of a circle and whose 3rd point touches that circle at some other point does describe a right angle at that 3rd point. That has only been assumed here though, not proven. Apologies if that comes earlier in the book.
For a while i used a 12 foot or inch depending on aplication after studying the Egyptian crafts man. That is suposidly how they layed out the pyramids.
I left the word atring out. Sorry i got distracted while I was typing.
Great bit of history there. Very entertaining. I did not know that a 10 foot pole was actually a thing. I grew up the response to “I would not touch it with a 10 foot pole” as a rather crude modification of “I would not even touch it even with your pole”.
Not to sound like a cheapskate, but I love the free information provided in this blog. It is always interesting and helpful. Please keep it up for those of us who can’t afford the books.