As Aequus as Aqua

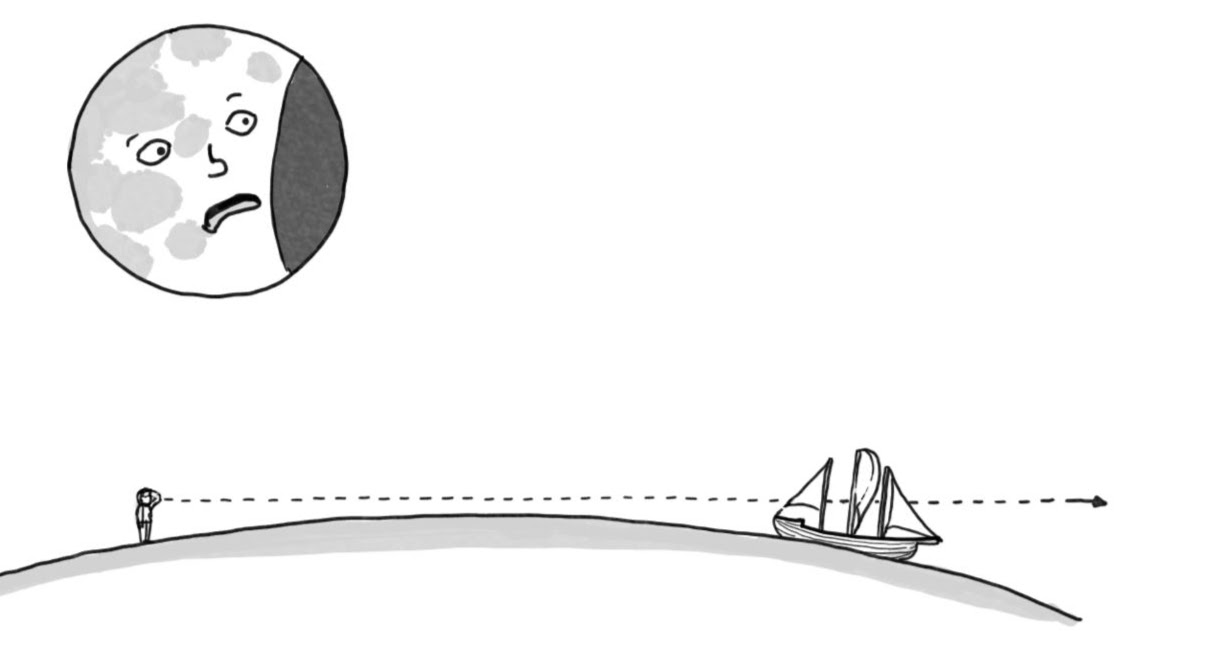
Or, translated from the Latin: “As Level as Water.” As we explored ancient layout tools at length in “From Truths to Tools,” it became quite clear that the artisans of antiquity were no dummies. For example, we see from their tools and works that they understood that there was a difference between the curved “level” of a horizontal line and the straight “level” of a sight line. In fact, when they used the term “horizontal” to name the latter they were alluding to “horos,” the horizon, the boundary between water and sky.

How did they know that the earth they stood on was a sphere? Two things for starters, according to source documents: They observed the arc-line shadow of the earth falling on the moon during a lunar eclipse, and they watched ships disappearing on the horizon from the hull to the top of the mast (as opposed to the ship simply getting smaller and smaller). Why is this so important? Try building an aqueduct so it works properly or digging a tunnel accurately through a mountain without accounting for this difference.

If the trough of the aqueduct were constructed to a sight (or laser!) line level, the water would flow toward the center because the center, relative to the earth’s surface, is downhill from either end. Another problem that could arise if the support columns were constructed to meet the trough at right angles, is that the columns would only be plumb in one location. They would all be parallel, but that doesn’t make them right! (Literally: the forces on the un-plumb columns would have some amount of shear in them, leading eventually to distortion and ultimately failure.)

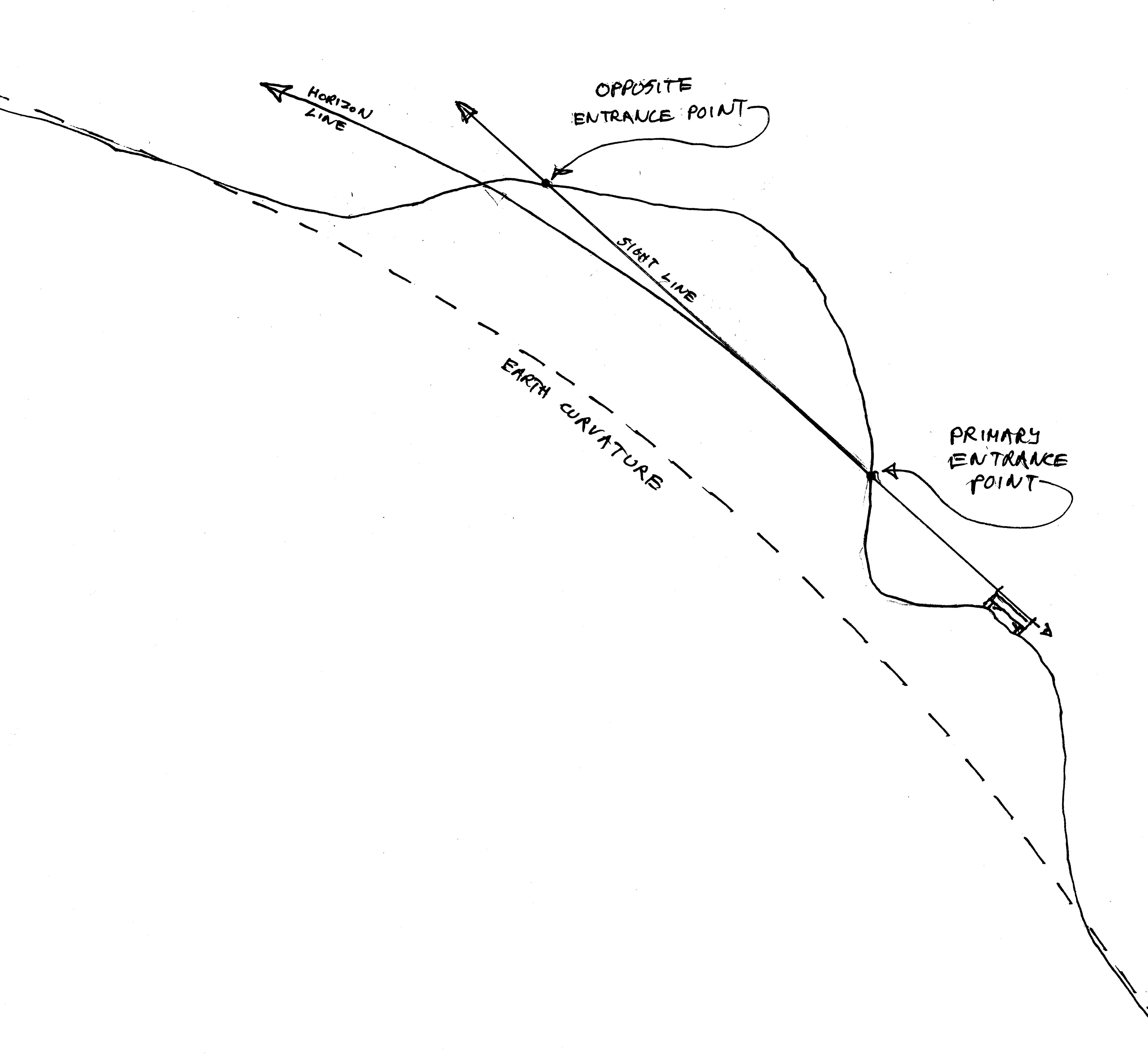
In tunnel work, the opposite problem arises: if they relied solely on horizontal level as the digging progressed from start points established by sight lines shot around the mountain from surrounding benchmarks, the tunnel would not exit at the predicted opposing point. Digging from either end, one tunnel would travel above the other and they would never meet. Note that the gradient drop of the earth’s curve is about 8′ per mile – and it’s not an additive (linear) increase, but exponential to infinity. To grasp this intuitively, picture the earth constantly curving away from the sight line. Eventually, at a point just past a quarter of the way around the sphere, a line dropped down square from the sight line would never reach the earth’s surface.

The more George and I immersed ourselves in research for this book, the more we gleaned about the tools and works of the artisans of antiquity and the smarter they started looking to us. The corollary was the dumber the guys in the mirror looking back at us each morning started to look! Obviously, not only is there is still so much more to learn, there is so much more to relearn!

— Jim Tolpin, byhandandeye.com