Well that’s not entirely true, of course. I do use them when I need to make up a cut list from a full-scale drawing or story stick to tell a machine in numerical code (be it metric, Imperial or shaku) where to make the cuts. The cut list is, however, rarely necessary in the hand-tool approach to construction. So in typical layout work, I go with pin-point perfect real placements of cut or location lines.
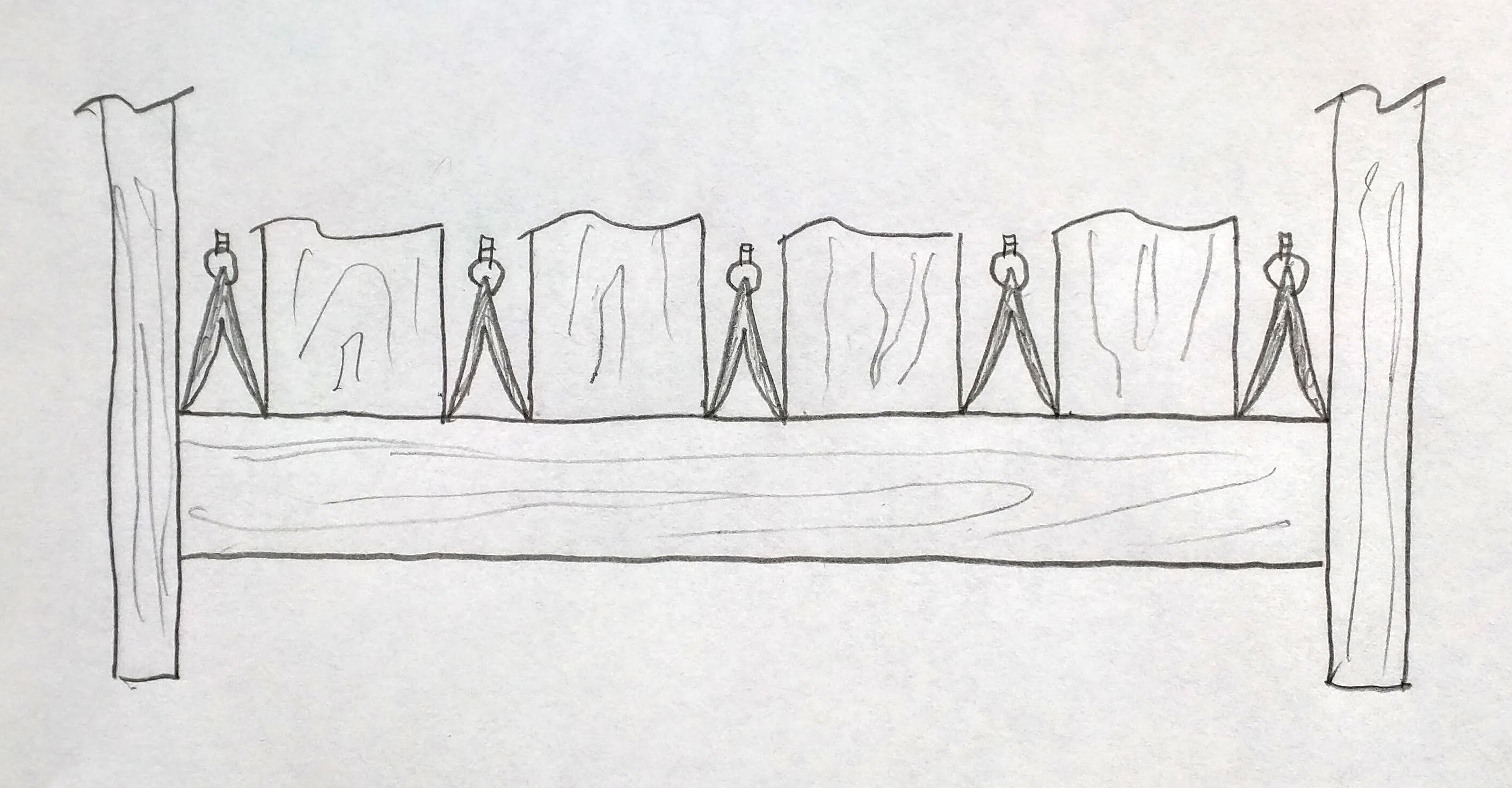
For example, if I need to lay out the location of slats in a bed’s headboard, I simply stack the slats together against the post (or its location on a story stick) and find the intervening gaps by stepping out the number of gaps needed between the slats (number of slats + one). Layout follows as shown in the next drawing. The accuracy of the layout will be a function of however sharp I make the points of my dividers.
Of course, you can use algebra to generate dimensions with numbers:
As for me, I don’t want to spend the time doing it and then having to deal with reading tiny numbers on some ruler and coping with rounding errors!
As another example of rulers not always ruling: Say you want to locate placement buttons (the ebony plugs in the set shown here) on a pair of winding sticks so you can quickly locate the sticks on the edge of a board. In this case, the location is not a number at all (at least not until after the fact). You could, of course, measure the length of the sticks and divide by two to get a numerical center point. Or, to avoid rounding error, you could step off an even number of intervals to locate the middle division line and then enjoy the accuracy of a pin prick. But both would miss the point so to speak. What we are really looking for here is not the center of the stick, but its center of gravity. How do we find that? We just balance the stick on a sharp knife blade!
— Jim Tolpin, byhandandeye.com and one of the authors of “From Truths to Tools“




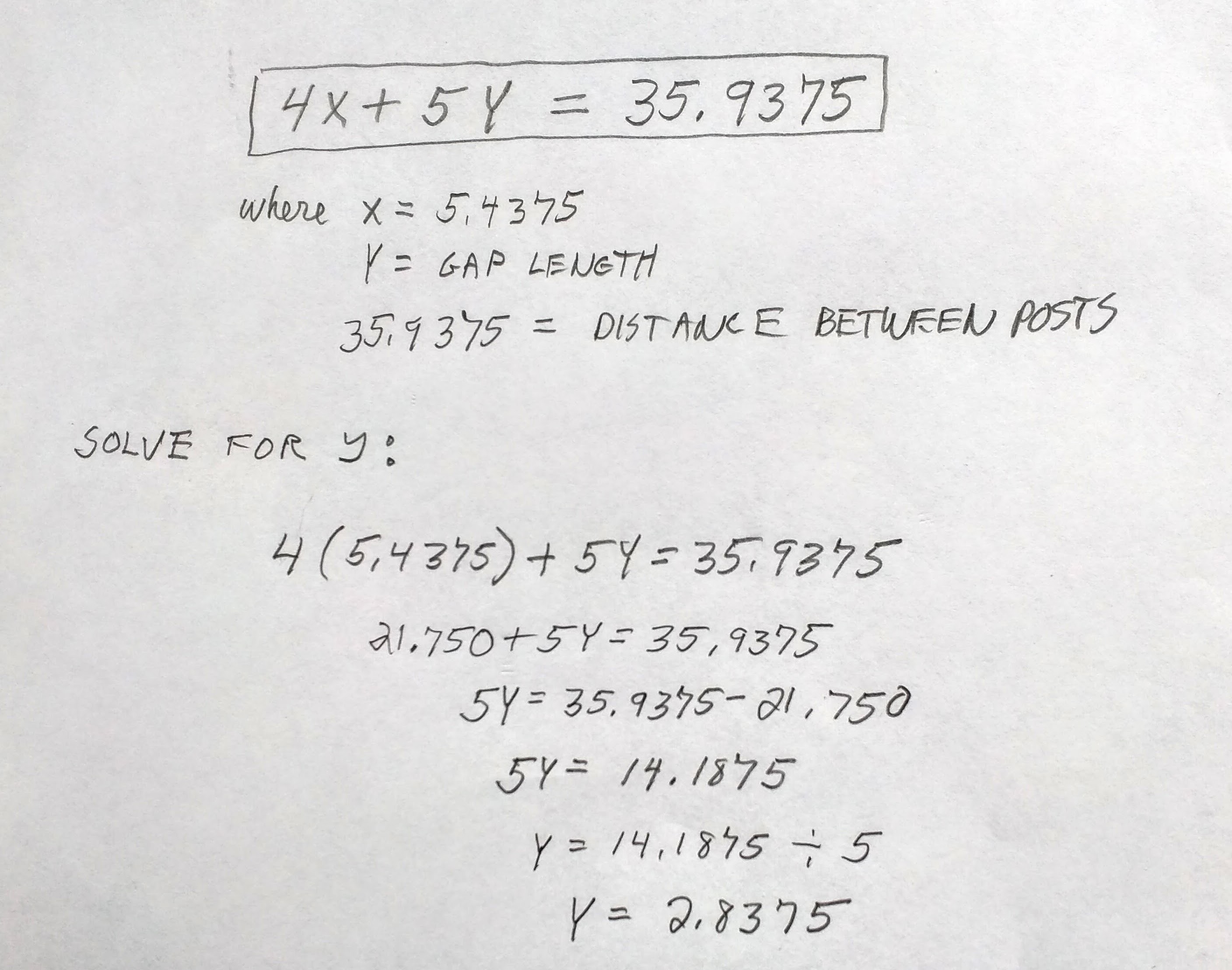

I love this method of working and and the books you guys have written on the subject. I’m just beginning to build with it so it isn’t automatic for me yet. I just completed a saw till using dividers and story sticks. It’s the first time I’ve hade everything come out perfectly square on the first try. I got the doors perfect fit and square the first time as well and didn’t have to fuss around mounting and trimming them multiple times. I’m a convert for sure.
I’m fascinated by this subject! I do struggle with all the cipherin’, though. It doesn’t help that I spent more time trying (unsuccessfully) to impress the ladies in math class than I did learning why there are letters AND numbers in some equations. But I bought all three of your books (as I do with all LAP books). I’ve already spent some serious bathroom time with the two I have, and I think I’ve gotten measurably smarter. (I would say measurably lighter too, but I don’t do potty jokes.)
I use the rule because I cannot retain the algebra needed between the times I use it. It is quicker for me to use dividers or just simple division and a story stick. For some reason long term memory of seldom used facts more than 6 moths old other than the Kardashians eludes me. Thank God for Google.
In your book on ancient geometry do you discuss the level? As as lifelong woodworker and collector of antique tools, I have wondered why one never sees examples (even in museum collections) of any of the levels that carpenters and cabinetmakers used for millennia prior to the invention of the spirit level and its manufacture after about 1830. I assume most woodworkers made their own, but they must have found the spirit level so much more accurate, easier to use and transport, that they trashed what came before. I have found precious little about them online or in my books on tools. I have done finished computer graphics of the six styles I have come across (which vary greatly from simple to complex) and have just finished an accurate working example (equilateral triangle style) which I am sure is more elaborate in material and finish than what most woodworkers of the past would have made for their own use.
Richard: We do indeed address the level in From Truths to Tools. In ancient times the Romans used them extensively. Instead of alcohol (spirits), however, they used water as the indicator of “horos” (horizontal). The tool was called a corrobate (probably from the Greek root word for confirm). Interestingly, it is clear they fully understood the difference between a level line and a straight line. We have illustrations of all this in the book
I am aware of the water pan method. The Egytians illustrated the wooden (non-spirit) level used in masonry and woodworking in tomb paintings; the same are also found in medieval illuminations. Would you be interested in the diagrams/illustrations I have of six styles of levels that carpenters – as opposed to builders and masons – used through the 18th c.? Clearly anyone who made one would have to understand geometry as well as the utmost accuracy in carpentry.
Surely would be interested! You can email me through byhandandeye.com
I find your use of dividers quite interesting. I’m a retired engineer and used them a bit in high school drafting but have never cottoned to them. The method you show obviously works for you but if I did it, I’d somehow find a way to mess up the divider setting or have cumulative errors impact the intended precision.
I think I would be inclined to find the center of the slats and then divide up the head board rails into equal segments. I’d do this using the old trick of parallel divisions (my term) and I’d be using a rule throughout without noting any measurement. I’ve shown this below. To perform, one takes a rule and sets a convenient exact spacing (in this case 3 inches) setting zero on one edge and three on the other edge and putting a mark at one and a half — thus dividing the slat exactly in half. I’d then transfer this down to the bottom of the slat.
I’m a little confused because your photo has 5 vertical slats and your computation has 4. I’ll assume 4 since you based your computations on that.
I’d use the same method for the rail. In your case, you have the somewhat over-derived 35.9375” between posts and a slat width of 5.4375″ (I’d be surprised if all five slats were this exact dimension). So the total width to be divided into 5 spaces is 41.375. The next highest number easily divisible into 5 spaces would be 45 with 9 inch increments. So I’d take a thin cut-off of sufficient length (although a tape measure could be used, it would be awkward) and tick of 9 inch increments. I’d probably mark this at 1, 10, 19, 28, 37, and 46 to avoid using the end of the cutoff. You have to add half the slat length to each side and I’d do this using one of the slats I’d center-marked to put a line on the corner posts representing a half slat width. I’d then line up each end of the cut-off measuring stick with these lines and transfer the marks, giving myself five exact divisions to be transferred up to the top of the rail and to be matched up with the center of the slats.
I could make a mental mistake with this method so I’d line up the pieces to see if they looked right. I’d also run a quick check. Five goes into 41.375 inches about 8.275. Subtracting off the about 5.44 slat width gives 2.835″. This is quite close to your number of 2.8375 and can pretty much be done in one’s head. Like 8.3 – 5.4 = 2.9 “ which is reasonably close.
The point to all this is there are easy ways to use rules and get exact results without using any but the very simplest math. I’d have more confidence in the results than those obtained with a dividers because this method eliminates cumulative errors.
BTW, if I were to make a set of winding sticks, I’d make the stick an exact, easily divisible by two, length and put the button in the center. If it was, say, 16 3/8 long, I’d put the button at 8 and cut off 3/8” from the long end. I don’t think I’d need to find the center of gravity if the wood was reasonably homogeneous.
Hope I haven’t been too snippy or made a silly mistake in my explanation.
Take care,
Mike Perovich
>