
Over the recent season of political and social angst I’ve been finding solace in research and development work with my co-author George Walker. While our fellow countrymen argue the gray areas of morality and policy, George and I have immersed ourselves in the immutable truths that underlie the first principles of geometry. While there might be some gray areas in a few of the tradesmens’ layout shortcuts (which we explore at length along with the fundamentals in our forthcoming book “From Truths to Tools”), the core geometric constructions of reality that flow from the intersection of line and circle not only represent perfection – they are perfection.
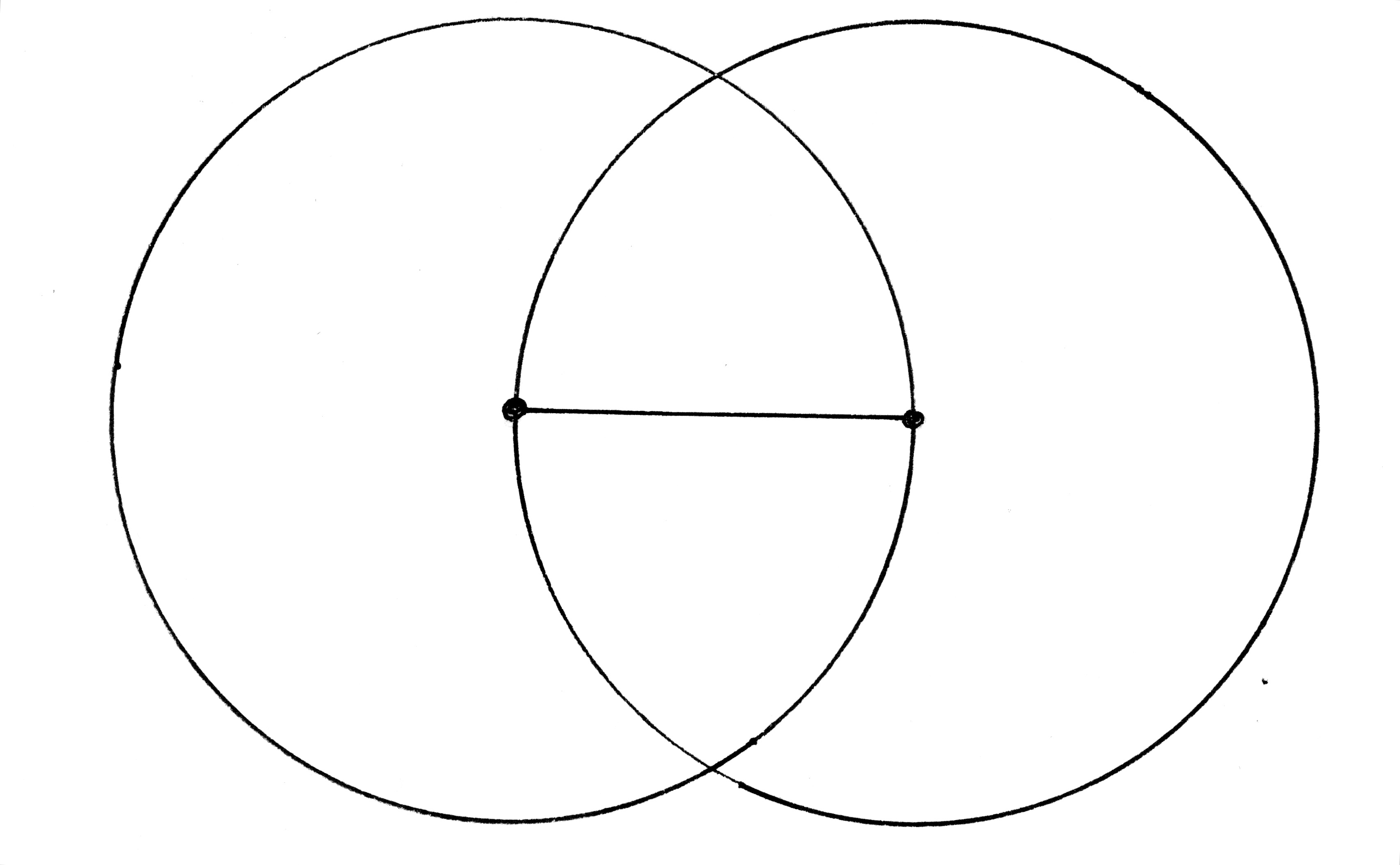
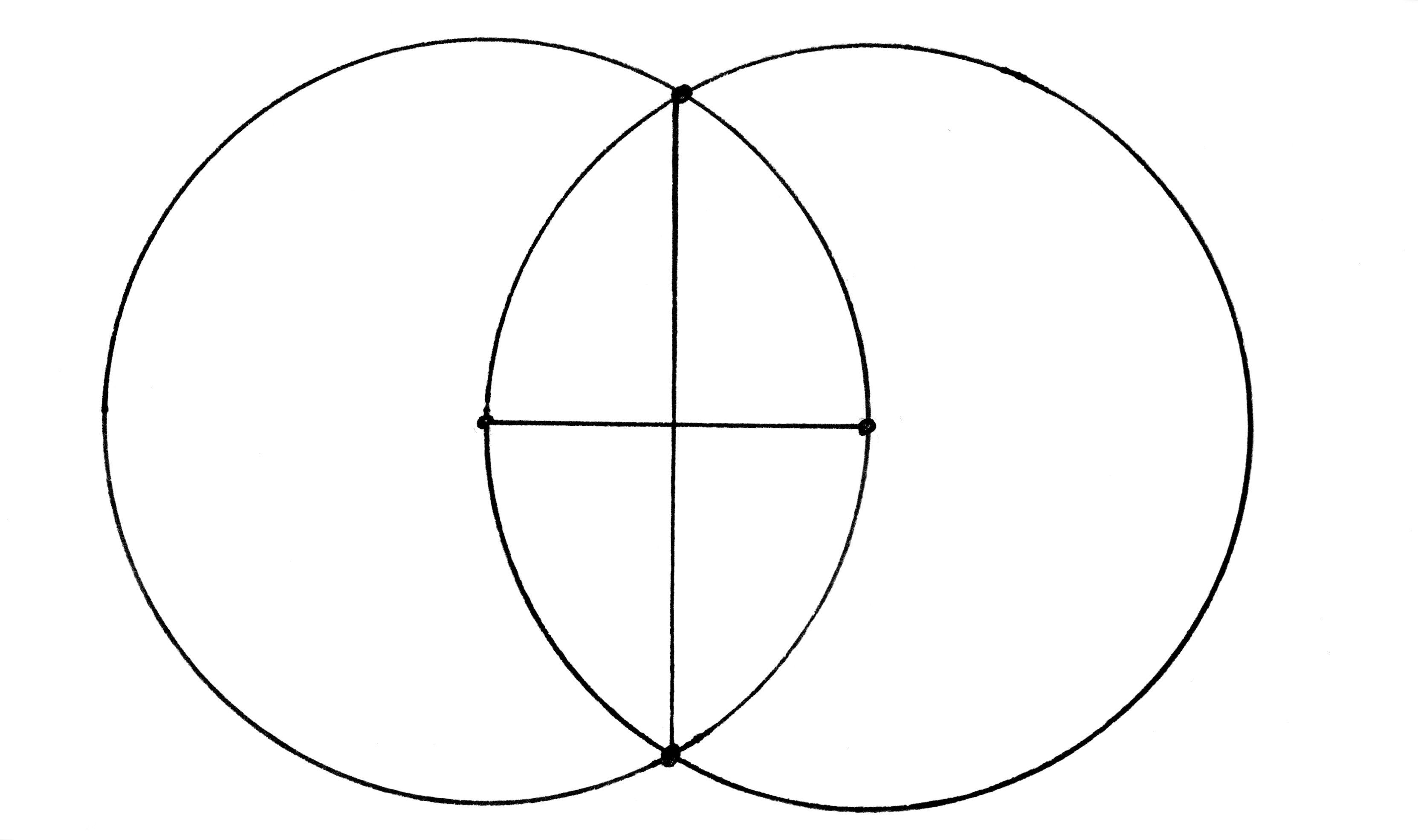
For example, two intersecting circles that share a common radius will present us with two rim intersection points to which we can connect a line that automatically – and unequivocally – “bi secare” (cuts in two) the shared radius line.
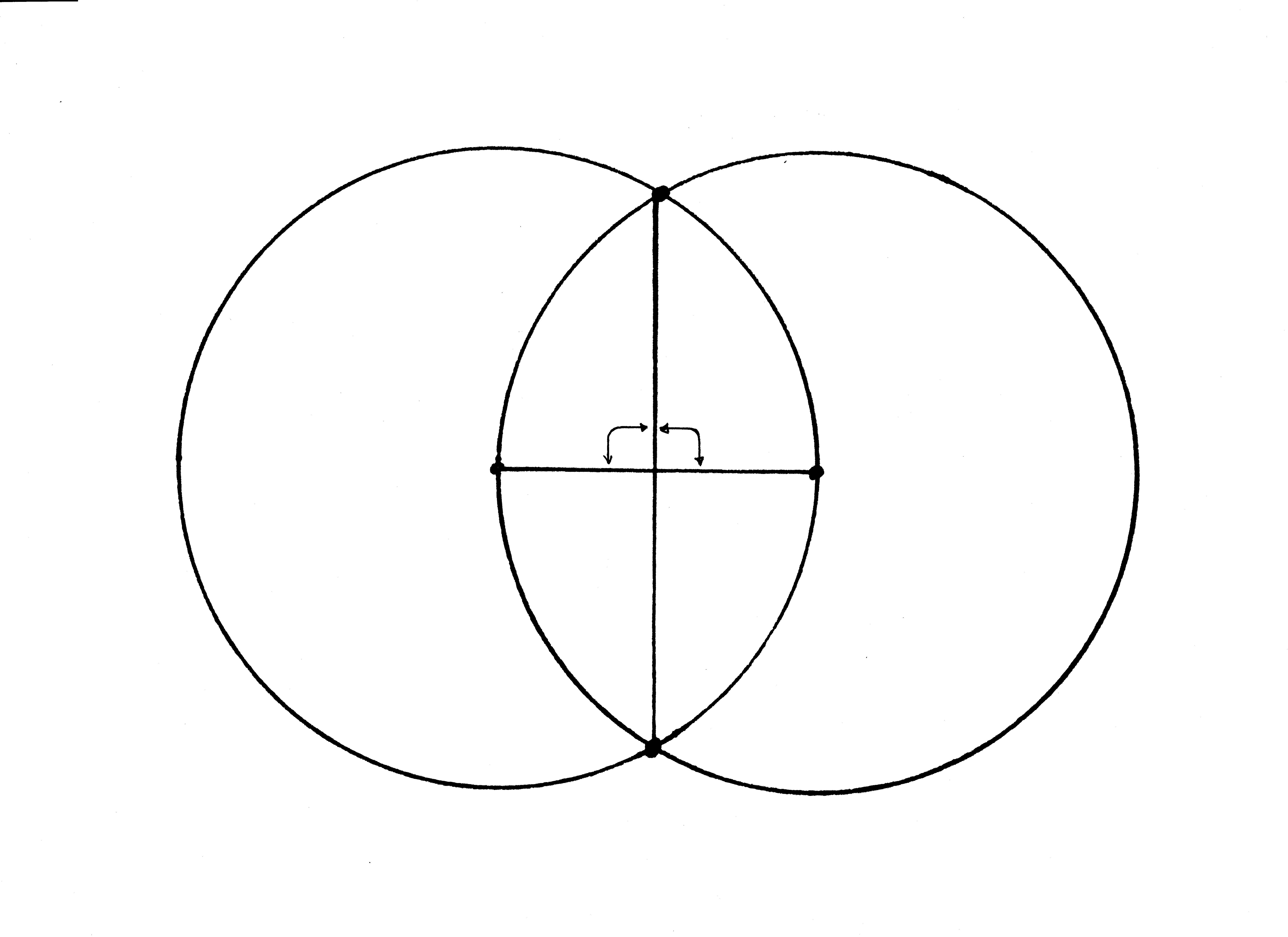
The intersection of the lines at the bisection point form a “rectus” (right) angle with the radius line. We know it’s a right angle because the other angles are “co-rectus” with one another and any two of them form a straight line.
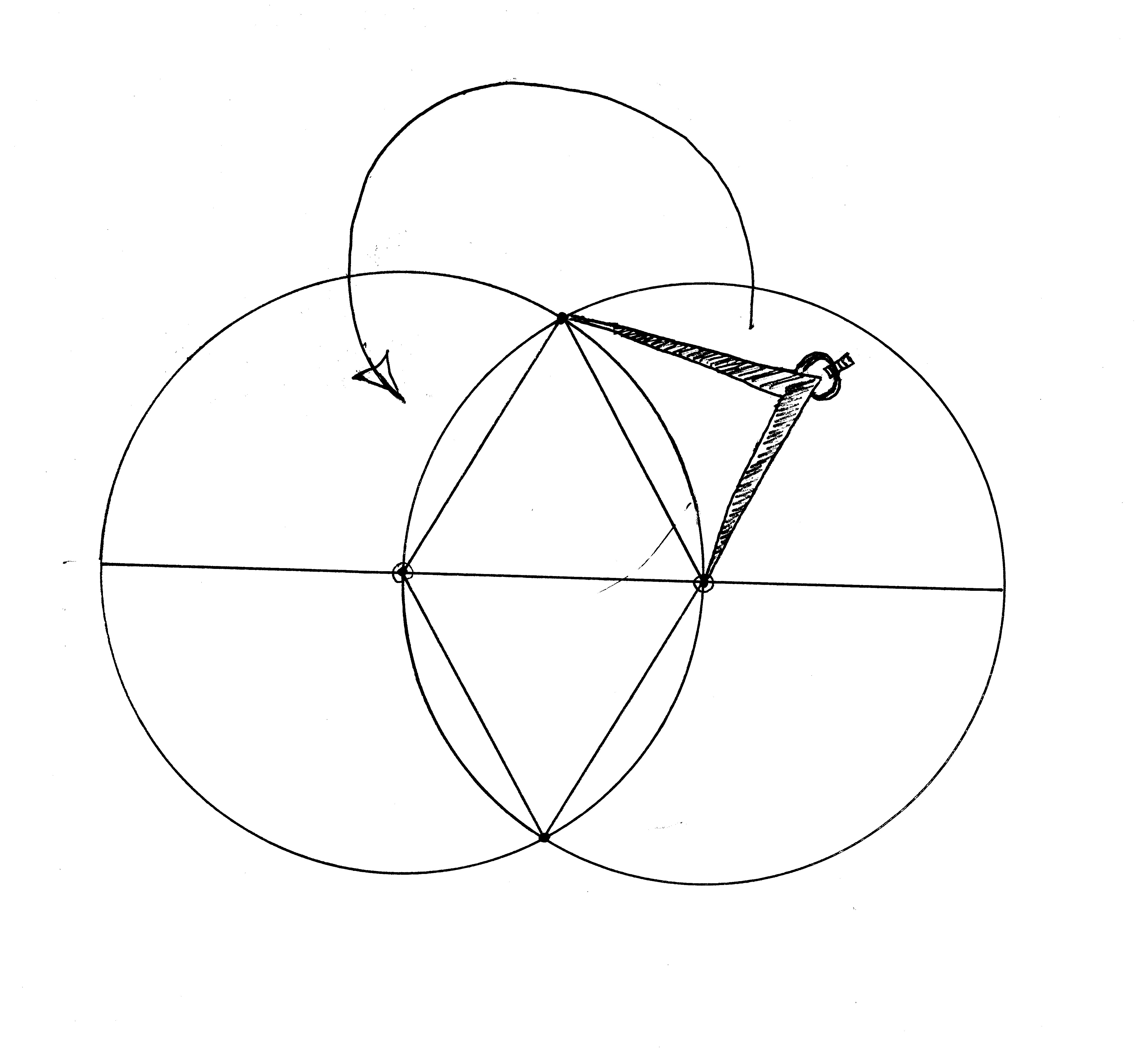
A further “proof” of the correctness of the four angles can be had by using dividers to “demetiri” (measure-out) between one circle’s focal point and a rim intersection point. This dimension will be exactly, precisely, perfectly the same at each of the other three point spans. This immutable truth provides us with the geometric construction we need to make a try square as well as the key to testing the tool for true. We now have in hand the ability to accurately lay out everything from a cradle to a coffer to a cathedral with little more than a bunch of sticks.
— Jim Tolpin, ByHandandEye.com

Interesting. After looking at this for a moment, I recognized the method I learned in high school for bisecting a line with a perpendicular one. We just didn’t draw the entire circles.
I’m with you, Joe. Seem to be no epiphanies here, just an unearthing of what we all should have remembered we learned in school.
While it’s true that we all learned about constructing that perpendicular line, that method is in fact the shortcut. The intersection of two circles having the same radius is the underlying basis, or “truth”, of that application. I think that’s what Jim and George are showing in this book. The shortcut is not a wrong approach, but it is derived from some discovery. The discoveries lead to many useful methods.