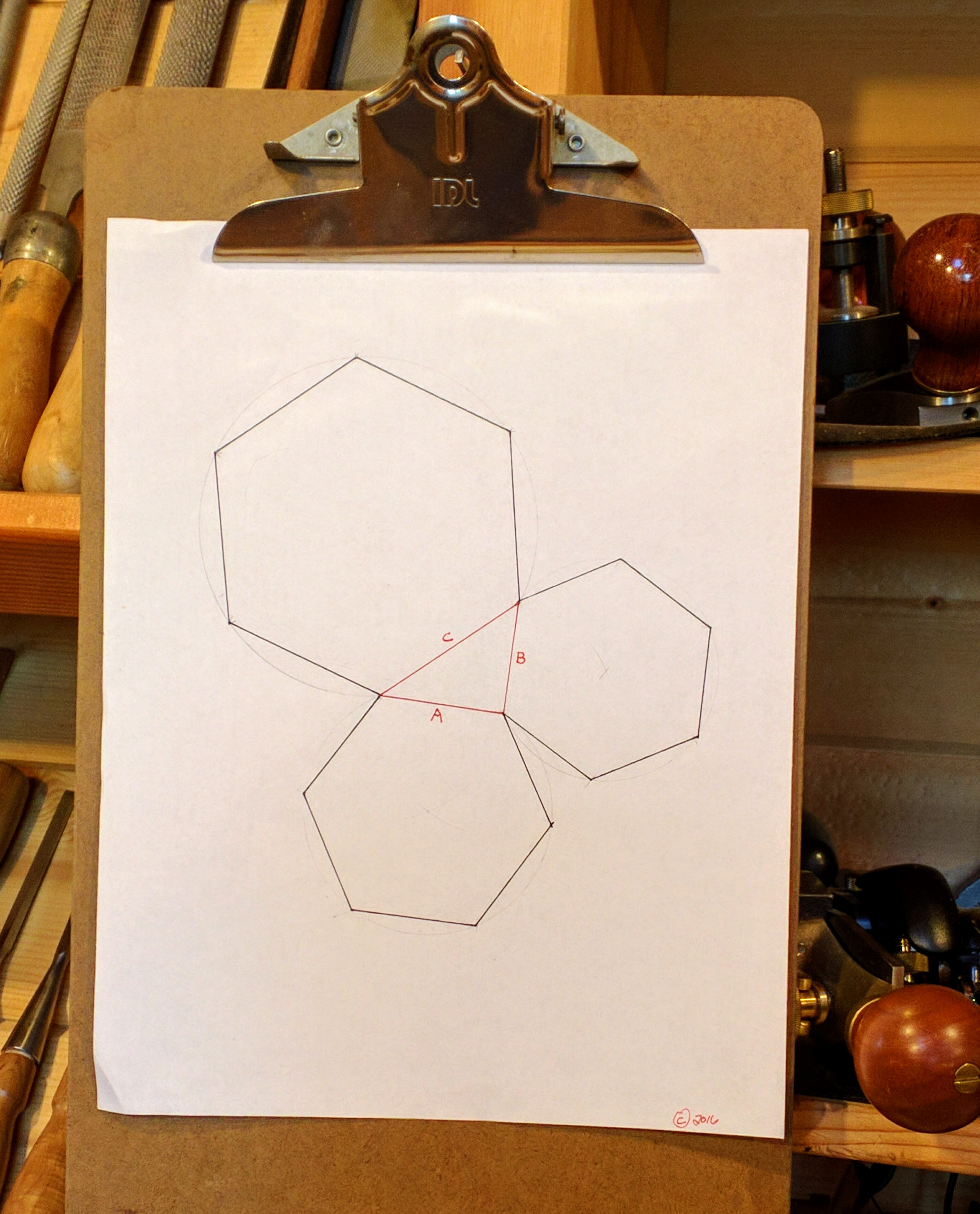
We (and our kids) were all inoculated with enough Geometry during middle school to “know” the Pythagorean theorem. You know, the one that enables us to rattle off: “A squared plus B squared equals C squared.” But that particular manifestation of the underlying geometric truth of our particular universe isn’t limited to squares. In the above drawing, we have three hexagons built upon the three legs (labeled A, B and C) of a right triangle. Just like squares, if you add the area of the two little shapes they will equal the area of the biggest one. In other words: A hexagoned plus B hexagoned equals C hexagoned. This works for all similarly shaped polygons by the way.
Want the “proof?” All you need is a couple sticks and a bit of string as in the photo below. Have your 4-year-old lend you a hand…she’ll immediately intuit what an equation is really all about! (No, this is not your rigorous algebraic proof, or even a Euclidean logic proof…Instead it’s what me bandmates used to call: “Good enough for rock and roll.”)
– Jim Tolpin, ByHandandEye.com


Seeing relationships between mathematics and the real world and visa versa is wonderful.
I found this app/game to be a fun discovery into how, just using a straight edge and a compass, one can find a perpendicular line, halve an angle, draw a quadrilateral with equal sides tilted at a 45 degree angle, find the midpoint of a line, find the exact center of a circle, etc, etc. No measuring or guessing, just using those two tools.
https://www.euclidea.xyz/
That’s pretty cool. Dynamic geometry apps do a great job of explaining things because they let you see how geometric principles apply in general rather than to a particular fixed construction.
You might like Geogebra too. https://www.geogebra.org/ it has great tutorials and many examples to learn from.
This is cool, but not as mysterious as it looks at first glance.
The rigorous proof is pretty simple as far rigorous proofs go and goes along way towards explaining what is going on.
X(A^2 + B^2 = C^2) = XA^2 +XB^2 = XC^2 (A^2 means A squared if that’s not clear)
X in this particular case is approximately 2.6 or the ratio of the area of a hexagon to the area of a square of the same edge length.
It works with any shape, not just polygons. It would work with the Lost Arts Press logo too, whether its bevel were up or down.
It would work if those hexagons were replaced with hexagonal prisms too if they were all the same length. All that would mean is that everything would be multiplied by an additional length factor L
LX(A^2 + B^2 = C^2) = LXA^2 +LXB^2 = LXC^2
While I appreciate the efficiency of numeric methods as an engineer, I cannot deny the beauty of empirical methods. Look at the architecture of Gaudi and the weighted string models he use to design buildings. I am still in awe even after knowing the mathatics.