In this sketch I did of a Masonic “Past-Master’s Jewels” medal, notice the representation of the pythagorean theorem. It is reported that its presence on the owner’s medal indicates that person was what we would likely now call a crew foreman. One of his many responsibilities was to ensure that all the layout tools were true – a clue as to why there’s the homage to Pythagoras. This theorem, codified later by Euclid into his “Proposition 47,” offers a logic proof that the area of the squares erected on the legs of a right triangle would equal the area of the square erected on its hypotenuse. That’s all well and good, but why would that particular equation be of vital interest to the foreman of a joiner’s or mason’s crew? To try to find out, I decided to construct an exact-as-possible, large-scale drawing of the graphic upon which I could explore with a pair of dividers.
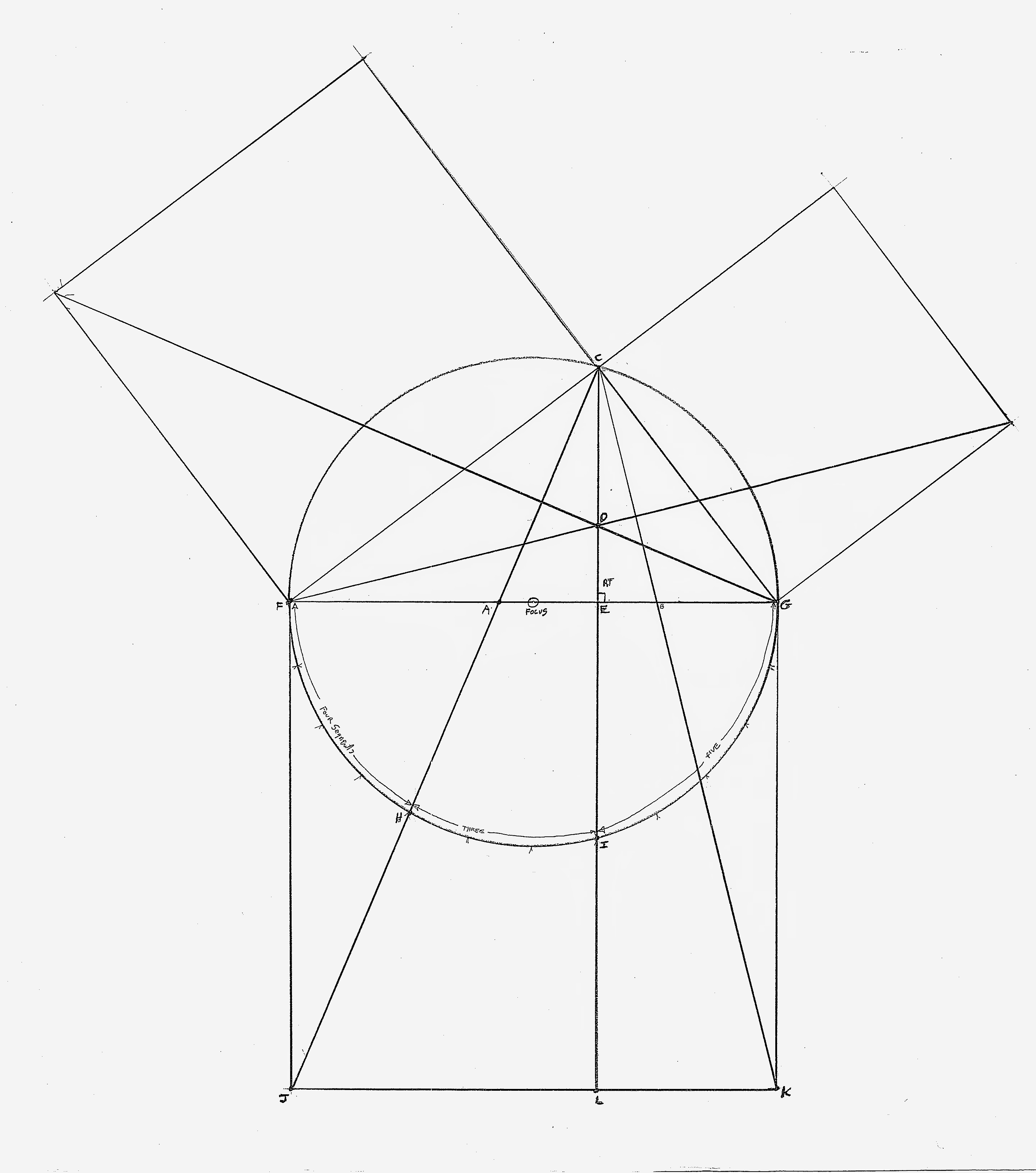
The first thing I discovered was that the vertical line CL, which is fixed by the inherent baseline’s intersection points C and D, forms a right angle with the hypotenuse. Even though this result is likely nothing more than symbolic (there are a lot easier ways to generate a right angle with a compass and a straightedge), I believe this right angle – hidden in plain sight – is probably as important to the medal (and its wearer) as the theorem itself. The right angle (“recto” in Greek) is simply the right way to set a vertical post. (Wood’s superb resistance to compression happens when, and only when, the post is set at a right angle to level – an orientation that aligns the grain parallel to the force of gravity). It’s also the right angle to create symmetry to a baseline in common rectilinear structures (think cathedrals).
No reason to stop there, though. Exploring further revealed other attributes of this graphic that offer additional symbolic (and real) representations of the truths inherent in Geometry (note the traditional capital G). Print out the template (you’ll find it offered for free on the shopping page of www.byhandandeye.com) and take a look around on it for yourself. You’ll discover triangles with perfect 2:3 base-to-height proportions (one of the fundamental harmonics in music and architecture of the Medieval era); you’ll find sequences of the infamous triplet (the 3-4-5 triangle) revealed in the hypotenuse and even in the circumference of the circle that started it all; and you may find the module upon which the entire construction revolves. Have fun with this – I sure did!
– Jim Tolpin, ByHandandEye.com
I recently joined the Mason’s and that geometry is referred to in the blue lodge text as the forty seventh problem of Euclid.
And so it is. The figure shown is a duplicate of the figure use to illustrate Proposition 47 in Sir Thomas Heath’s 1908 translation of the Elements (mirrored around a vertical axis).
For the purposes of the proof, it is less important that CL be perpendicular to “the side subtended by the right angle” and more important that it is parallel to the two sides of square JFGK and creates the two parallelograms JFEL and LEGK. The gist of Euclid’s proof is to identify two pairs of similar triangles (like Mr. Tolpin says, keep looking and you’ll find them) and prove that the pairs are congruent as well as similar – and thus have equal areas. With this property in hand, he uses an earlier problem (Proposition 41) to show that the area of the smaller square is equal to the smaller parallelogram (LEGK) and the area of the larger square is equal to the area the larger parallelogram (JFEL). Sums of equals are equal, Ta Da!! – or QED, as they say.
James Garfield – our 20th President – was a bit of a mathematician as well as a speculative mason. He produced a proof in 1879 that relies on similar properties of triangles and parallelograms; but uses different line work.
When I started at the trades, the notion that someone would pay me good money just to solve a geometry problem (and then build it) pretty much blew my mind. I’m happy to report that it’s still that much fun.