Students, friends and mental health professionals have asked me how I became interested in researching old crap through books, paintings and by rebuilding vanished forms.
They expect an answer like: “Oh, I’ve always liked history” or some such. That’s not true. I hated history until college.
The real answer is this: In 1986 I read page 101 of Michael Baxandall’s “Painting and Experience in Fifteenth-century Italy” (Oxford). That did it.
OK, that’s an exaggeration. It was actually pages 95-101.
Starting on page 95, Baxandall begins a discussion of the “Rule of Three,” a common way to solve simple commercial math problems. Here’s an explanation by Piero della Francesca:
The Rule of Three says that one has to multiply the thing that one wants to know about by the thing that is dissimilar to it, and one divides the product by the remaining thing…. For example: seven bracci of cloth are worth nine lire; how much will five bracci be worth?
Today we might represent this equation as 7:9 = 5:X, but that’s a fairly modern way to represent the idea. Earlier merchants would line up the parts of the equation like this: 7 9 5 (result).
So why is this a big deal? Many in the merchant culture used this equation every day. It was so familiar that they made jokes that played upon the proportional relationships of numbers.
“The merchants’ geometric proportion was a precise awareness of ratios. It was not a harmonic proportion, of any convention, but it was the means by which a convention of harmonic proportion must be handled,” Baxandall writes.
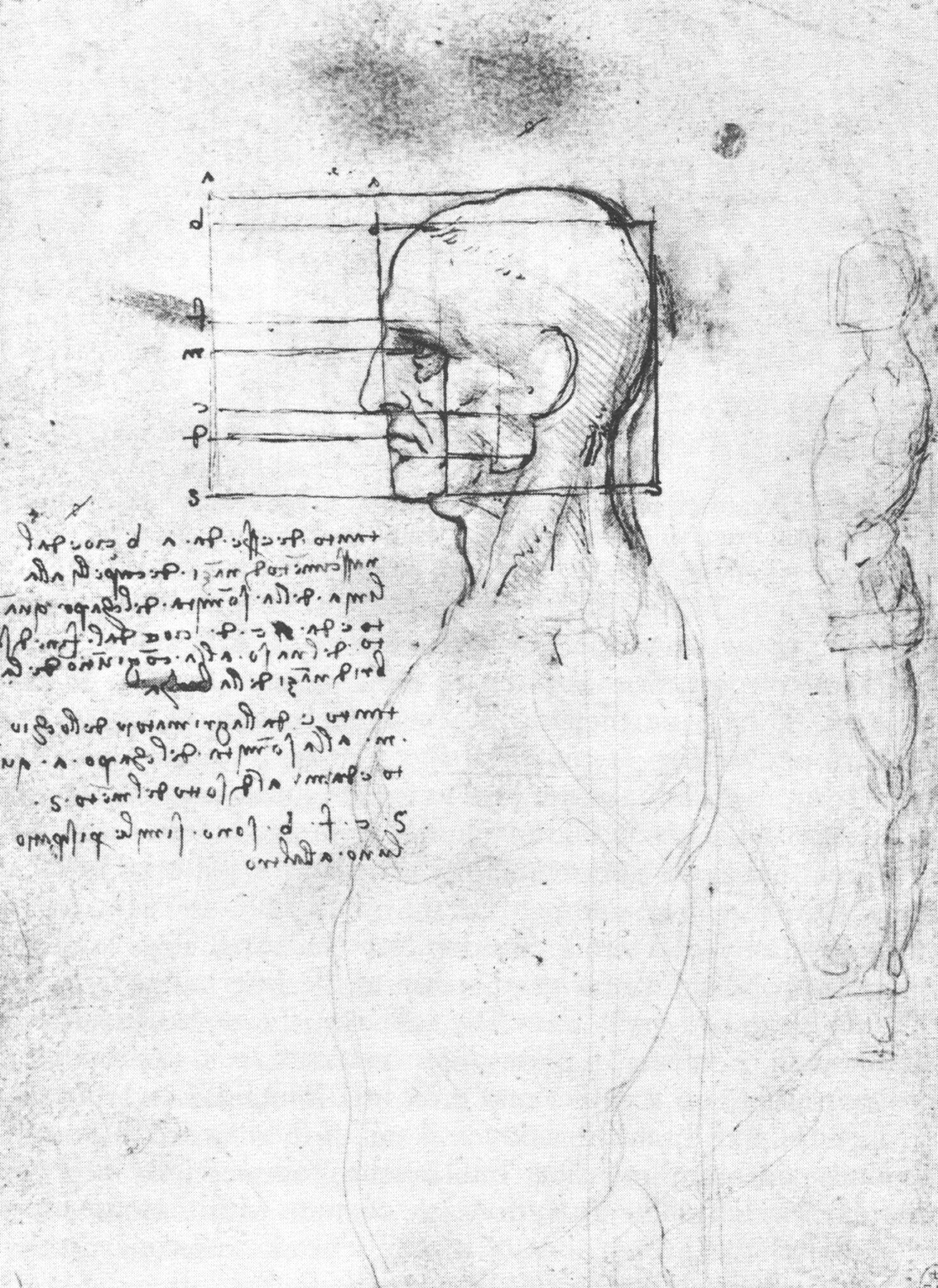
Such as Leonardo da Vinci’s “Study of the proportion of a head.” Baxandall writes:
…Leonardo is using the Rule of Three for a problem about weights in a balance, and comes up with the four terms 6 8 9 12: it is a very simple sequence that any merchant would be used to. But it is also the sequence of the Pythagorean harmonic scale – tone, diatessaron, diapente, and diapason…. Take four pieces of string, of equal consistency, 6, 8, 9, and 12 inches long, and vibrate them under equal tension. The interval between 6 and 12 is an octave; between 6 and 9 and between 8 and 12 a fifth; between 6 and 8 and between 9 and 12 a fourth; between 8 and 9 a major tone. This is the whole basis of western harmony.
And so I was hooked. Was this true? Do these relationships show up all around us?
— Christopher Schwarz


Absolutely.
The pentatonic scale has been in use for at least 40,000 years.
http://www.ethanhein.com/wp/2011/flute-of-forgotten-dreams/
This is interesting; I’ve read more ancient and renaissance mathematics and physics than the average man on the street, and I can’t recall a rule of three being explicitly mentioned, which makes me think it must have been more of a utilitarian mnemonic for laymen. It is absolutely true, though, that mathematics before the modern era was defined not in terms of numbers but ratios, and the ancients were much more conscious of ratios as the comparison of similar quantities. A renaissance mathematician would find the statement of the cloth problem as 7:9::5:x absurd, because it’s impossible to have a ratio of cloth to lire; the only way to approach the problem is to say that 7:5::9:x. Also, if the order of items is supposed to be A x B/C = result, shouldn’t the order for this problem be 9 5 7?
Never mind–I see the traditional formulation involves multiplying the second and third items in the series and dividing by the first.
Methinks CS has been hanging around the Woodwright shop much too long!
Can you explain more as to how this can relate to furniture design? I think of music and how everything is 3 chords – 1st, 4th, and 5th – and I could use that simplicity, I could design pleasing furniture. Make sense?
Well, they are whole-number ratios. And I think that is a basic backbone to thinking about furniture.
We have two books on this topic (sorry for the commercial). “By Hand & Eye” and “By Hound & Eye.”
734 : 5592341 is a whole number ratio. That says absolutely nothing about its use in either a particular design nor design in general.
1 : √2 is the ratio of a whole number and an irrational number. It’s readily findable in classic art and design the world over. Yes, it is all around us, almost certainly including the proportions of various elements of a number of letters on this page.
I have these books and have read them – I of course buy everything that you sell – that’s what Anarchist do…… Granted, I have not done the exercises. The compass and pad are waiting – but I am missing something, and maybe I am looking for too much – it’s not clicking in my head – all these ratios – and when you do the math on a plan from in a magazine or otherwise – they never come up with these ratios or simple ratios – they come close if you count using hand grenades as close.
What should be the ratios be for 3D design – and I know what you are going to say – it’s up to you and etc. – that’s the point.
But with ratios, you can still design turd that you thought was going to look right because you used 1:2 for the sides 3:5 for the end and etc…. Anyway.
Mark F., look at Jim’s projects in the back of By Hand and Eye. They might help bring the ratio thing home.
I don’t expect anyone to catch the fever, but By Hand and Eye is easily the best book I have on woodworking. Funny part is, most of the book is applicable to any making/designing endeavor.
I still suck at woodworking, but that book makes me suck less.
My ‘Rule of 3’ is: If I have 3 of something in the workshop, I can find one of them in less than 5 minutes, but if I have less than 3 it takes an hour or more, often weeks, and much cursing and swearing. Not exactly mathematical but true.
the golden ratio 1 to 1.6 works for me. but the rule of 3 make sense
Well, I’ll swallow my pride and cop to not understanding a word of this. I don’t see it. What’s the ‘3’ part of the ‘Rule of Threes?’
In the ‘bracci of cloth’ example, what ‘thing’ is the ‘thing that one wants to know about’ and which ‘thing’ is the ‘dissimilar’ one? I can solve for X, but don’t see the point. What am I missing?
That’s exactly the problem I am having.