Pins or tails first? Yes, it’s that eternal question, once again: If you overload a dovetail joint, which will fail first, the pin board or the tail board? I was inspired to take a closer look at this after reading a comment posted to Chris’s Popular Woodworking blog a while back: the poster was concerned about the strength of the skinny little pins in so-called London Pattern dovetails. Chris’s response (which was the correct one) is that it doesn’t really matter, because dovetail joints are generally overkill for what they’re meant to do.
But it does beg the question: Can you make your pins too skinny? What about your tails? To get some insight, I fired up the finite element analysis engine once again. But before we get to that, a brief refresher on stress and strain (you did take engineering mechanics in school, right?). You can skip to the juicy stuff if you get bored.
When we apply a mechanical force of some kind to a chunk of material, we exert a stress on that material. If the material deforms because of the stress, the deformation is known as strain. There are a variety of different kinds of stresses and strains; for analyzing dovetail joints we’ll concentrate on two: tensile and shear.
Tensile stress occurs when we push or pull on our material in a direction perpendicular to the surface:
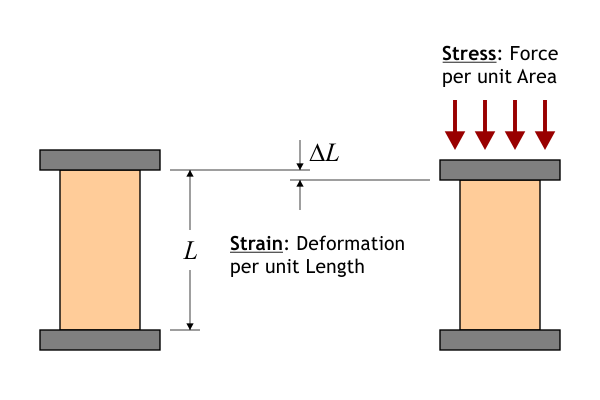
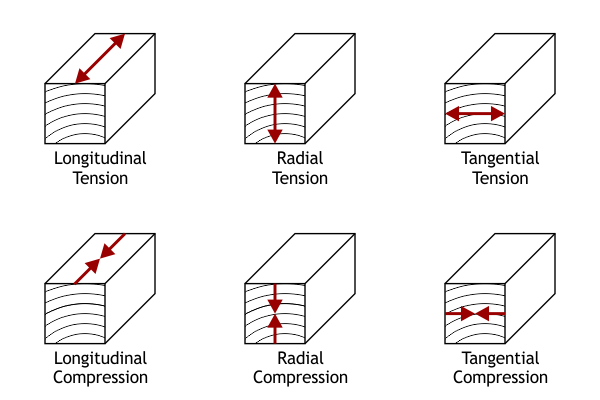
As long as we don’t exert too much stress, the relationship between stress and strain is linear: double the stress, double the strain. The ratio of stress to strain in a given material is known as the modulus of elasticity, or Young’s modulus. Because wood is anisotropic (it has different mechanical properties along different axes), we need to keep track of three separate elastic moduli, one for each of the major axes (longitudinal, radial and tangential). Finally, we can apply either tension or compression along each of those three axes, so there are six basic kinds of tensile stress that a piece of wood might have to endure:
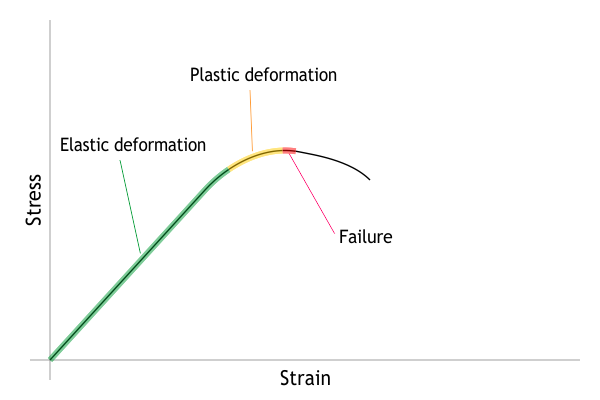
Speaking of elastic behavior, a typical stress/strain graph looks like this:
The other kind of stress that we need to know about is shear stress. In contrast to tensile stress, shear stress is applied parallel to a surface:
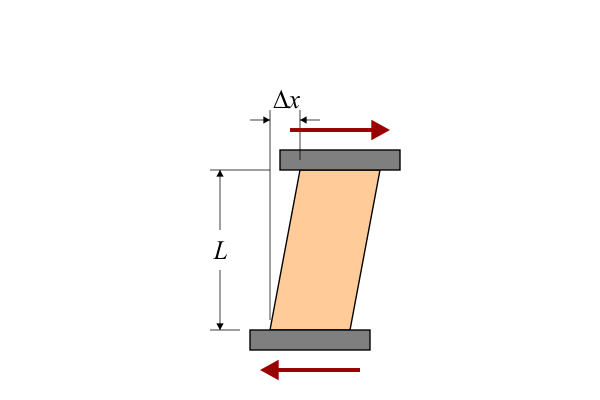
The ratio of stress to strain in shear is known as the modulus of rigidity, or shear modulus. As with tensile stress, we need three separate shear moduli, and we need to consider six different ways of applying shear to our material:
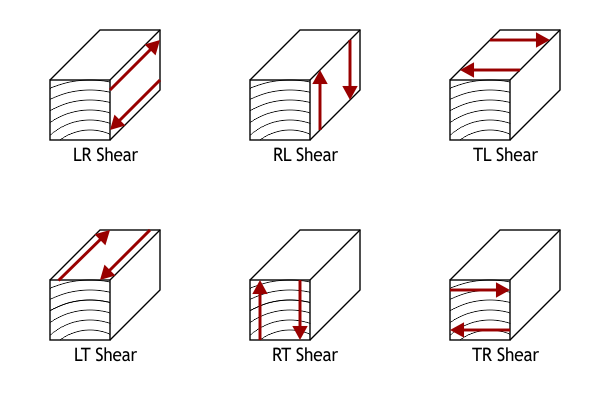
LR and LT shear are the two kinds of longitudinal shear. Wood is generally more resistant to longitudinal shear than rolling shear; however, longitudinal shear is a common failure mode in an overloaded beam.
Finally, RL and TL shear are the two kinds of transverse shear. Except for certain brittle softwoods, like western redcedar, wood very rarely fails in transverse shear: it will undergo tensile failure first.
There is one final complication to all of this: When we pull on a piece of material, in addition to getting longer, it gets skinnier. Conversely, when we push on it, in addition to getting shorter it gets fatter:
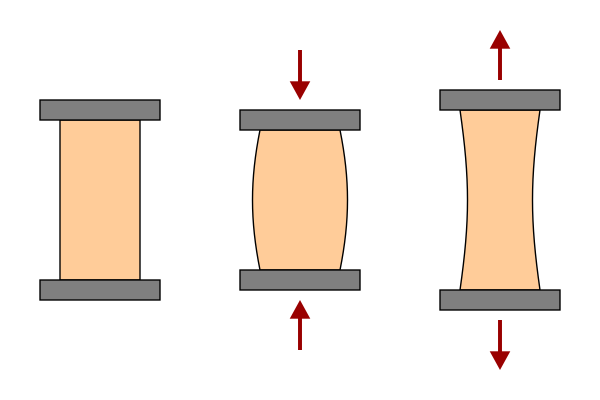
So, when we model the mechanical behavior of a wooden structure, we have to take all of this into account. (Fortunately, we just have to specify the nine material properties; the modeling software does the rest.) For this investigation, I used values for dry black walnut (values for an assortment of woods are listed in the Forest Product Laboratory’s Wood Handbook). I modeled the joint as two quartersawn boards, 12″ L x 4″ W x 3/4″ T, with a single large dovetail (1:8 slope). For this simulation, I used Calculix software, and the joint was loaded as if I were trying to pull the tail board straight out of the joint.
The result for the worst-case tensile stress in the tail board is shown here:

The result for the pin board looks like this:

Maximal shear stresses are shown below; they are concentrated in the same areas:

The most important takeaway from these images is to note how the stresses are very tightly localized, right at the joint surfaces. The bulk of the material in both tails and pins is just sitting there doing nothing useful. That tells you that skinny pins (and skinny tails) are just fine. In fact, if you’re concerned about the strength of a dovetail joint, a solution would be to use as many pins and tails as you can cram into the width of the joint; that way, any destructive forces are spread out over more joint surfaces:
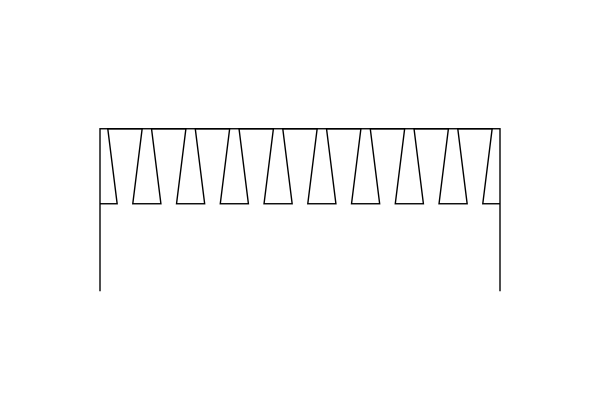
So who wins, pins or tails? As it turns out, the peak tensile stresses are very close in the two halves of the joint. Given that the wood is quartersawn, I’d have to declare the tail board as the victor, since its major stress component is in the radial direction, whereas for the pin board it’s in the tangential direction. However, if the boards were flatsawn, it might very well go the other way.
Of course, in a real-world hand-cut dovetail joint, one of the tails or one of the pins will inevitably be tighter than the rest, and that’s where the failure is going to occur.
–Steve Schafer



Lovely analysis. Thank you.
Where was the juicy bit?
That was just a ploy to keep you reading. Sorry.
That said, if you’re coming to Lost Art Press for juicy bits, I might suggest that you’re in the wrong part of the Internet.
🙂 steve, this is one joint being pulled straight out – did you look at how things change when the board being pulled is dovetailed at each end?
Ha! Brutal honesty…
I’d like to extend the analysis to more “real world” conditions, like racking and such, but the complexity goes up quite a bit, and I don’t know how well the software will be able to cope with it.
I feel smarter(er) 🙂
What happens if you add glue to the equation?
yay cause the glue is stronger than the wood , right?
In the case of the simplified scenario shown here, probably not much. The failure modes are tensile failures in directions that wouldn’t be helped by glue. But in the real world, I’d expect glue to help in at least two cases: One, racking stress in a dovetailed box or carcase; glue would tend to prevent the joint faces from sliding against each other. Two, excessively thin half-pins (or half-tails); because the stress on a half-pin or half-tail is asymmetric, there is a tendency for it bend away from the stress, which gluing would counteract.
I don’t know offhand how glue is modeled in these kinds of simulations. It seems like you could model it as a very high coefficient of friction. I’ll have to do some more research…
Thanks for the reply Steve. If I followed you right I think were pretty much on the same page for effect. I hope to see your thoughts with some more research in hand.
Great explanation of stress and strain. I wish my UC Prof had been so clear at the beginning of the quarter. From a purely engineering point of view, the way to reduce the stress at the root of both the tail and pin is to introduce a radius at this point. An old mentor used to say that “Mother Nature doesn’t like sharp corners”. This is of course overkill for a wooden dovetail joint, but wouldn’t that look interesting. What a challenge to cut: get out the gouges.
If we restrict ourselves to hand-cut joints, then I think the added complexity wouldn’t help much, because you’re limited more by the relative perfection of fit of the joint. And the more complex the joint, the harder it is to get a good fit. For a machine-cut joint, I would assume that there is an optimal profile that achieves maximum strength for a given species, grain direction, etc. I leave that as an exercise for the reader.
After 42 years in engineering, this retired reader will pass.
How cool is this? I feel I have arrived. I posted the question on one blog post that inspired an entirely new one.
Thanks for the detailed response. So now to incorporate it into the current build.
ZZZZZZZZZZZZZZZZZZZZZZZZZ
Agreed. I’d rather be cutting dovetails rather than talking about them. This type of in-depth examination is what is known as “Analysis Paralysis”.
For those who disagree with me, however, this was a very thorough explanation of something woodworkers figured out hundreds of years ago without computers.
No, it’s not analysis paralysis. You could call it “overanalysis” (which would be a fair criticism), but analysis paralysis is an entirely different phenomenon.
Note that “something woodworkers figured out hundreds of years ago” also has a name: conventional wisdom, rules of thumb, etc. The thing about conventional wisdom is that it’s usually right, or at least close enough to right. And that can lead us into the trap of thinking that it’s always right.
If you’re content with replicating what has already been done before, then following conventional wisdom will probably serve you well. But if you’re trying to do something new, you can very quickly find yourself in a situation where conventional wisdom fails you. And the usual reason that that happens is that conventional wisdom tells you What, but it very rarely tells you Why.
Understanding the Why is where theoretical analysis comes into play. It allows us to extend our knowledge beyond the existing wisdom, and create new knowledge that can be applied to new problems. I recommend Henry Petroski’s To Engineer Is Human for a good introduction into the interplay between theory and practice, and how both are required in order for us to learn new things.
In 1958 some folks performed the experiment on wood, rather than software: http://www.akeda.com/documents/DovetailAngle.pdf
Very briefly, unglued joints tend to compress the tails and pop free. Glued joints tend to sheer the edges of the tails and rip free. Glued joints fail sooner than unglued joints.
Theirs were all nice and uniformly machine cut, but I’m guessing the same failure modes apply, and in any case the width of the tail still seems irrelevant.
That’s very interesting. One difference to note is that they tested half-blind joints, and the main difference there is that there is more “meat” in the pin board to withstand tensile failure across the width of the board.
I’m not surprised that the greater compressibility of softwood resulted in a high level of compression failure in the tails. I’ll have to look at how changing the material properties affects the simulation.
“Finite element analysis engine”, that’s the thing in the Batcave with the little amber wheelie thingy and flashy lights that Robin was always using right?
Mine has blue LED lights, but you’ve got the basic idea.
Wood is anisotropic, and some woods takes easily a dent. So I expect to see for these well behaved woods lots of plastic deformation while still being mainly in an elastic stress mode. That could give fairly different stress peaks.
I don’t understand the secondary site of stress in the dovetail.PIN image, i.e., the stress down the board from the joint. It seems to me that this stress would not be there if you pull the joint apart in the opposite direction from the way it goes together, that is, “pull the tail out of the socket”. If you pull the joint apart by pulling the pin board out of the tail board, that is, perpendicularly to the way the joint goes together, the result would be far more catastrophic.
If I understand your question correctly, the pin board is rigidly fixed at the far end. Therefore, as I pull on the tail board, it causes the pin board to bend. That’s what causes the high stress in the bulk of the pin board.
Great stuff, Steve. Was this a nonlinear analysis?
Part 2 – Dovetail fatigue failure!
Nah, im guessing it was linear elastic.
No, as Bob says, it was a linear analysis. Except for a couple of thoroughly studied species that are used in structural applications, like Douglas-fir and southern yellow pine, there just isn’t enough published information to do a real nonlinear analysis.
That is a great analysis…it just so happens that I had a car wreck, with a dovetailed box, filled with cutting boards in my trunk. The box cracked a bit: the car that hit me was probably going about 35-40 mph and the box was filled with cutting boards (combined weight of about 35-40lbs); I think he cutting boards slammed into the ends of the box that cracked. However, the joints didn’t fail; the wood did…you can see photos here: http://www.godetfurniture.com/?page_id=369
That’s a great photo. In your case, the wood failed due to impact, rather than a slow, steady force. Impact deformation and failure is generally much more difficult to model accurately.
Your box was tested in the other direction, not the same as the test above. You can definitely see that the gluing of the end grain didn’t help with the strength. The rolling shear of the tails was the weak point here.
Very interesting this 🙂
Steve,
What would you predict if the model did not use quarter-sawn wood? My gut tells me the results would be different, and that the stress point or region might shift. Also, what about old-growth vs. the new lumber we use today? I wonder if distance between growth rings might affect the results, in ways similar to what I suspect the medullary rays might affect the results. Only gut feeling, though.
Thanks for the excellent analysis; I learned that it is OK to make tiny/skinny tails and pins, and not worry about premature failure. However, I dislike the look of skinny tails and pins. I hope “disliking” does not change the results of the FEA.
I look forward to additional modeling, if possible, primarily with flat-sawn lumber, if you find a little free time.
Al Navas
You ask a lot of good questions, most of which are very difficult to answer. Regarding quarter-vs. flat-sawn, I did mention at the end that I’d expect a flat-sawn tail board to be weaker than quarter-sawn, and a flat-sawn pin board to be stronger, based on the fact that wood is a bit stronger in tension radially vs. tangentially.
Old-growth vs new: I can only do a simulation if I have good material properties data to draw on, and there doesn’t seem to be much in this regard. What does seem to be true is that when softwood trees grow more quickly, their density is lower, and their modulus of elasticity is lower as well. While that means that the overall strength is lower, it’s not enough information to tell us whether the failure mode of a dovetail joint would be affected.
Oak exhibits the opposite behavior: fast-growing oak is denser and stronger than slow-growing oak, primarily because of a reduction in the ratio of highly porous earlywood to latewood. An oak beam will fail in longitudinal shear along the earlywood rings, which are weaker than the surrounding tissue. And, of course, oak fails readily in tangential tension, largely because the extremely weak medullary rays act as stress concentrators.
I entered a *DISLIKE SKINNY PINS AND TAILS flag into the simulation, but it just told me that it couldn’t understand what I was talking about.
Old-growth vs new:
Indeed the MOE is lower, but the strength is not. Think of this: the sapwood of a tree has a lower MOE, but more strength.
But I do think that your models are not showing the correct results. The corners where the stresses are large, are modelled to sharp. And therefore the stresses will peak there. This is a common problem with FEM and sometimes hard to overcome. I can’t see how big your elements are, but if you would make them smaller in those corners you will see even higher stresses. I don’t know the exact word fore this in English, but is a common term en FEM.
I know this is hard, wood and FEM are hard to combine. But if you would use the plastic range of wood in compression. I’ll bet you would see a different failure mode and conclude that skinny pin are weaker then big ones. The shear failure in the experiment noted above show a more realistic result.
So good work for putting this together! But we not there yet in terms of a defined conclusion.
You are absolutely correct about the perils of modeling sharp corners. I did take some steps to mitigate the problem. The results shown above are modeled using a random tetrahedral mesh (quadratic 10-node tetrahedra), and the mesh size at the joint faces is 1/16″, increasing to 1/4″ far from the joint. If I decrease the mesh size further, the peak stresses do go up, but I find that the other stresses do as well, and they continue to track pretty well (that is, the ratio of stress at a given point to the peak stress stays about the same). That tells me that I’m in a reasonably linear part of the model space.
Modeling plastic deformation would be great; there just isn’t much good data available. There’s a recent paper on modeling plastic deformation during transverse compression. Their experimental data is only for true poplar (Populus sp.), which isn’t very representative of the kinds of woods that we normally use for dovetailed joinery, but it’s a start. I’ll have to see if I can adapt their methods.
Finite element analysis always gives my inner mathematical modeler a boner. Where has my wife gotten to anyway…?
Nice work!
Isn’t the point of a dovetailed joint its ability to stay together for 200 years? And isn’t the drawer the primary place dovetails are employed? See here, Mathy Matherson, the horizontal stresses on a drawer are not large. The decay of wood, the loosening of nails, the warping of boards are the relevant concerns over long periods of time. Dovetails resist the forces of age because of their 3D configuration. Is max strength relevant? Inebriated minds want to know.
Maybe a little more modeling will answer your question, cooley. What I think about is a drawer full of cutlery in the china cabinet, or one full of heavy tools in the shop. That might change what happens to the dovetails over the 200-year period. And what about a till made with skinny dovetails and filled with not only saws, but a couple dozen hand planes?
– Al Navas
Never mind. Inebriated minds no longer want to know. They just want to lay down, here, under this park bench for awhile.
What the…..Not even thru my first cup of starter fluid and i actually got that! Who says it’s all downhill after fourty!
Thanks for the Great posts….
Interesting, though that I make things with dovetails and nothing has failed at that joint is good enough for me.
Awesome explanation! Love it!! Strength of Materials was one of the most useful courses I ever took. Why things break and how to prevent it!!