Chris gives you geometry homework; I give you partial differential equations:
This is the diffusion equation. It’s often called the heat equation, because it also models the diffusion of heat through a solid. And you’ll sometimes see it as Fick’s Second Law, after Adolf Fick, who first formulated it around 150 years ago. (The Wikipedia article on Fick’s Laws is a good introduction to diffusion from a physical, rather than abstract math, point of view.)
In our case, the quantity of interest, symbolized by u in the equation, is the moisture content of the wood. While it looks formidable, the interpretation of the diffusion equation is actually fairly simple:
Gradient: You have more “stuff” in one place than another, and stuff tends to move from high concentration to low concentration; the gradient measures the steepness of the slope.
Diffusivity: Also known as the diffusion coefficient, this is a property of the material and represents a sort of speed limit, controlling how fast stuff can move.
Divergence: This is a little trickier to wrap your head around: It measures the three-dimensional shape of the gradient. Imagine that you’re in a boat, bobbing up and down on a choppy sea. At a specific moment, you look around you and see that you’re on the crest of a swell, and the water all around you is lower than where you are. What’s going to happen next? The water underneath you is going to flow away in all directions; you’re in a spot with high divergence. Conversely, if you’re at the bottom of a swell, all of the water is going to flow towards you. That’s also a large divergence, but of the opposite sign. But if you’re on the side of a swell, even though there’s a gradient, you’re not going to move up or down because the water is going to flow right past you, from the high side to the low side. That’s a spot with very low divergence.
So now you know the key to surfing: Find a spot along the leading edge of the wave that has zero divergence, and just stay on that spot as the wave moves towards shore. What could be easier?
If the diffusivity of wood were a simple number, we’d be able to very quickly solve the diffusion equation for any specific set of conditions. Unfortunately, it is anything but. It seems to depend on just about everything, short of the phase of the moon:
Temperature: Diffusivity exhibits Arrhenius behavior, increasing rapidly as temperature goes up. (This is why kiln drying works.)
Density: Diffusivity is higher in low-density, lightweight woods than it is in high-density woods, so low-density woods dry faster than high-density woods. In fact, density is a pretty good proxy for species as far as drying is concerned: Woods of the same density tend to dry at the same rate (there are prominent exceptions, however; oaks dry more slowly than most other woods that are comparably dense). This also explains why extremely dense tropical hardwoods seem to never dry at all.
Orientation: Diffusivity is anisotropic, meaning that it has different values in different directions (the technical term is symmetric rank-two tensor). In wet wood, at moisture contents of 25% or higher, diffusivity along the grain is roughly 2-3 times as large as it is across the grain.
Moisture: Diffusivity is also a function of the moisture content of the wood. But it’s complicated: As the wood dries, the diffusivity along the grain increases (as long as the wood isn’t extremely dense), but the diffusivity across the grain decreases. At a moisture content of 5%, the disparity in along-the-grain vs. across-the-grain diffusivity in a medium-dense wood is a factor of 100 or so.
We’re going to use a technique called finite element analysis (FEA) to model the moisture flow through wood. (I’d give you a link to a good layperson’s description of FEA, but I have yet to find one that doesn’t immediately descend into esoteric math.) Suffice to say that FEA works as follows:
- Chop the problem up into a very large number of tiny little pieces,
- make some straightforward assumptions that simplify the equations within each piece,
- solve the simplified equations for each piece, and
- stitch the gazillion solutions all back together.
FEA is a technique that could not have existed were it not for powerful computers.
I’ve set up a web site at https://github.com/Steve-OH/lap_water where you can download all of the stuff that I’ve put together for this post, and run your own simulations, tweaking the parameters as much as you want to. I’ll leave the hard-core technical discussion to the documentation there, and just focus on the results of some simulations here.
The first problem that we’re going to look at is a simple workbench slab of white oak, 18″ wide, 96″ long and 6″ thick. The initial moisture content is 30%, and the equilibrium moisture content is 10.3%. Here are the results after a simulated 6 months (click to enlarge):
(The three panels represent cross sections of the slab cut through the center along each of the three principal planes, laid out like a conventional three-view mechanical drawing.) Note that the end grain is drying noticeably faster than the faces and edges. After one year:
Here, we’re starting to see the moisture-dependent change in diffusivity really take effect, as the end grain drying starts to take off. After two years:
And after five years:
At this point, the slab has lost most of its moisture, so the rate of moisture loss is slowing down considerably. Even though it’s not fully dry yet (the center is at about 13.5%), the slab is nevertheless “settling down” and further changes will happen slowly. The ends are much drier than the center, so they’ve probably cracked quite a bit from differential shrinkage.
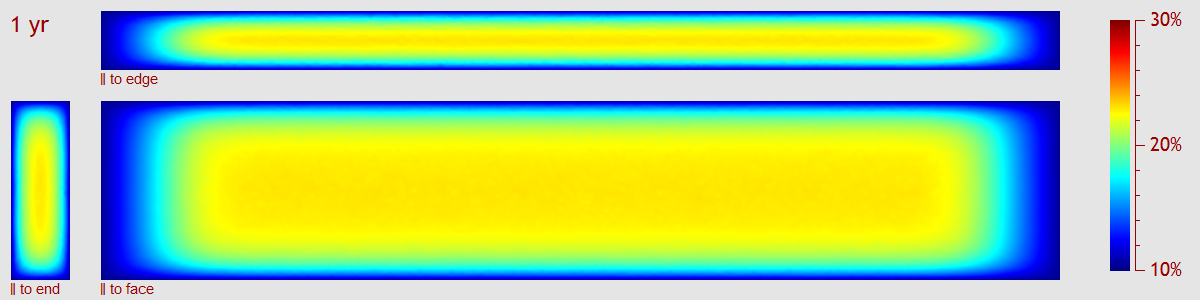
What about coating the end grain to slow down moisture loss and avoid major end cracks? I decided to explore that idea, but hit a road block trying to find published data on the diffusivity of water in wax (or any other candidate for end coating). So I used the best data I could find, and adjusted the thickness of the coating so that moisture loss through the ends was negligible. If you look at the simulation parameters, my model wax accomplished this at a thickness of 0.010”, but I think in real life you will probably need a thicker coating to get the same effect (i.e., my model wax is more impermeable than real wax). Anyway, here’s what it looks like at one year:
You can clearly see that we’ve stopped moisture loss through the ends. At five years:
What’s most striking here is that although we’ve completely sealed the ends, the peak moisture content in the center is almost exactly the same as it is in the uncoated case. So in the long run, the ends aren’t as important for drying a large slab as one might think; the take-home lesson here is that it probably always pays to end-coat a thick slab to prevent (or at least reduce) cracking, even if you’re in a hurry to dry the slab.
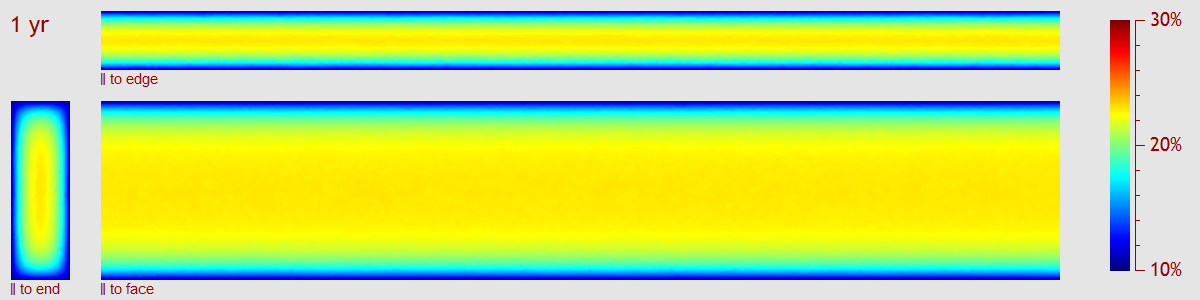
What about drilling holes in the bench to speed up drying? I modeled the simplest variation of this by means of a 1”-square hole, cut all the way through, smack dab in the middle of the slab. After one year:
And five years:
As you can see, the hole definitely works, but it’s also obvious that the effect doesn’t extend very far, so you’re going to need a lot of holes to adequately ventilate the whole slab. And, you’re probably going to get some end-grain cracks inside the holes, which certainly isn’t a good thing.
But even if you could do it, is it a good idea? Consider a simple thought experiment: Take a board, flat sawn and about 1/2″ thick and 8″ wide, and plane it nice and flat. Do the same with a 2″-thick board. Now wait until the weather turns rainy for a few days. What will happen to the two boards? The thin one will have an obvious cup in it, maybe as much as 1/16″. The thick board, on the other hand, will hardly have budged. The reason, of course, is that the thick board has more “moisture inertia.” In order to get it to move, you need to add a lot more water, over a longer period of time, than you do to the thin board.
And that’s the real advantage, from the point of view of stability, of a thick workbench slab: It has a lot of moisture inertia. So while it may take several years to fully settle down, once it has, it’s going to stay settled down. By drilling the slab full of holes, you eliminate that inertia. While you do speed up the initial drying, you also speed up its response to day-to-day changes in the weather. So it’s going to dry quickly, and then keep getting wetter and drier and wetter and drier forever.
Some of you may have noticed that the drying times in the simulations above are shorter than in the graphs I presented in the first installment of this series. Part of that is the result of what I mentioned above: the model is based on density, and oaks dry more slowly than other woods of the same density. But that doesn’t seem to be enough to explain all of the difference. I think the rest of the story involves free water, which, as I mentioned last time, is supposed to move freely through the wood, but might not in at least some species. Unfortunately, there appears to be zero published data on free water movement through thick oak slabs, so I may have to do the experiment myself: The next time I find myself having to fell an oak, I’ll sacrifice a few large, thick pieces in the name of science. Of course, it will probably take the rest of my life to amass enough data to be able to come to any conclusions, so don’t hold your breath.
One final caveat: As we all were reminded a few posts back, the map is not the territory. Models are useful for gaining an understanding of what’s happening in the real world, but they are simplifications. Wood is a complex, highly variable material. Don’t just blindly follow formulas when drying wood; use them as a baseline—a way to intuit what’s going on—but don’t forget to listen to what the wood is telling you.
– Steve Schafer

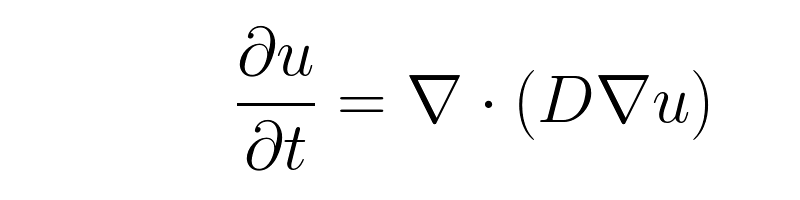






Yay! At last a woodworking question I’m fully equipped to answer. Chris has watched me wrestle with tools, but now he can watch me teach Diffy Q’s to sing.
But I’ve got a pile of mahogany paneling in the shop waiting to be repurposed…
This is an excellent post… definitions, assumptions, references, differential equations, finite element analysis… all of this and woodworking?! Well played Steve.
My head just exploded… Very cool that this can all be boiled down to a mathematical equation.
Did you ensure that your meshes ran to convergence? 🙂
In fact, I did run a number of preliminary simulations before settling on the mesh size. The mesh is actually overkill for all but the very beginning of the simulation, where there is a discontinuity in the surface boundary condition (fixed at EMC) and the volume initial condition (30% moisture), resulting in an extremely high gradient.
I could have eliminated that by specifying a more realistic (and complex) initial condition, but since it only affects the first few time steps, it didn’t seem worth it. I’m not going to lose any sleep over a discrepancy of at most a day or so, in a result measured in years…
Reblogged this on Tales from the Sugarbush and commented:
Ever wonder about the mathematics of drying wood? Look no further!
Thanks for doing this. I haven’t had a chance to use it yet, so please pardon my premature question. If one knows the tangential and radial shrinkage as a function of moisture content, can it predict the amount of cupping that will occur with a given thickness and width. My guess is no because it will depend on how the board is quartersawed, rift sawed, flat sawed, etc. Correct?
Sorry. I just read to the bottom of your webpage and answered the question above. It can’t do it at this time.
Shrinkage calculations are substantially more complex, for a variety of reasons (in order of increasing difficulty):
1) You can no longer ignore the cylindrical geometry.
2) Wood undergoes plastic as well as elastic deformation.
3) Wood cracks.
Crack initiation and propagation is way, way beyond anything I’d want to tackle. Plastic deformation is tractable, but there’s not a lot of published data to draw on.
I am so turned on right now. Nice job Steve; from a fellow (former) engineer and mathematical modeler…
I’ve retained enough higher maths to read the post, but willfully forgotten enough to just take your word for it. 🙂
If I read this correctly, your model reaffirms the one inch per year rule?
Nope.
Just for you, I ran a bunch of simulations for varying thicknesses. The results are at https://github.com/Steve-OH/lap_water/blob/master/dryingTime.pdf. (Click the “View Raw” link.)
Thanks for taking the time and running the simulation.
I assume, as in your blog post, the EMC is 10.3%?
Seeing how EMC is location and seasonally dependent, could you elaborate why you chose this number?
Excluding arid regions, in most places it is in the ~12% -14% range.
http://www.fpl.fs.fed.us/documnts/fplrn/fplrn268.pdf
In the model, the EMC is not specified directly, but is computed from the relative humidity and temperature.
I’m still thinking in terms of a slab workbench in a shop, so I used a relative humidity that was on the low side (55%). If we increase the humidity to 68%, then the EMC becomes 12.9%, and the drying time goes down somewhat (for a 6″ slab from 30% to EMC+0.5%, from 11.8 years to 8.6 years). Of course, the drying times for both thinner and thicker slabs goes down correspondingly as well.
In practice, you can get a much more substantial effect by raising the temperature than by raising the humidity (especially assuming that you’re eventually going to bring the wood into a fully conditioned space). Sticking to the original 55% humidity but raising the temperature from 52°F to 72°F, the drying time decreases to 6.8 years.
You speak of overestimating drying time, but do you really think it is possible to air dry a 2 inch oak board to EMC in a year as your chart suggests?
Well lookey there. My physics major might come in handy in my woodworking!
…..glad it had pictures.
It’s great seeing the differential equation, understanding what it says and then thinking: “Hey, wasn’t this LAP, the site about resuscitating almost-vanished woodworking practices?” Anyway, I love the way that all the math and interesting simulations essentially boil down to “Bigger is better”. That’s my kind of engineering!
Math and woodworking how could it get better or my heart get any warmer????
Ok, money for fancy lumber to build a campaign dresser….
Just one thing I have been wondering about:
Why does the moisture content in the wood adapt to the relative humidity in the air, and not the absolute humidity?
That’s because the relative humidity gives the actual amount of water relative to the amount of water that the air could contain at the given temperature and pressure. So depending on the relative humidity it’s easier to add water vapor to the air or remove it. That ease is what influences the net transport of water into and out of the wood. If it’s easier to get water into the air than it is to get it into the wood then your wood will dry. If it’s easier to get water into the wood than into the air then your wood will get wetter.
In a sense, it doesn’t really matter whether you choose relative or absolute humidity as your variable, since there is a well-defined relation between the two (as a function of temperature). Choosing one or the other just changes the equations a bit. People tend to use relative humidity because (a) it’s easier to measure, and (b) various humidity-related properties tend to track relative humidity more linearly than they do absolute humidity, for the reasons that Arthur elucidates.
To add a bit of technospeak: The balance between moisture in the air and moisture in the wood (or other material) is called the sorption isotherm. This is the basis for Table 4-2 in the Wood Handbook (http://www.fpl.fs.fed.us//documnts/fplgtr/fpl_gtr190.pdf) that shows the relationship between temperature, relative humidity and moisture content.
The reason that I was not able to more accurately model the wax coatings in some of my simulations is that I couldn’t find sorption isotherm data for any waxes.
Cool ! This blog was the last place, I expected to see a differential equation 😉
I’m with the other diff eq lovers. Nice to see. I need to review what I’ve kind of forgotten about diffusion and anisotropicity. I also never found Arrhenius satisfying (it works, for sure) when it came to actually explaining why it works, but that’s why we have materials scientists right?